Mass m oscillations with conductivity

[diracdelta]

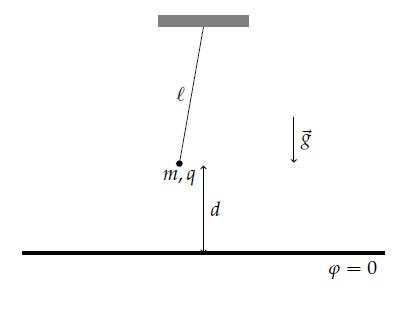
Sphere of mass m, and charge q is hanged on a thread of length l in a constant gravitational field g.
There is infinite horizontal conductive plan which is kept at potential 0.
Find period of small oscillations of sphere.

So my question is next, how do i get the force due tu charge q in Newtons equation.?

 

[DuckAmuck]

If the bottom surface is a conductor, then there will be an image change of -q. You basically treat the conductor like a mirror. So now in addition to gravity you have attraction between charges.

So the force on the sphere will roughly be:
F = mg + kq^2/(2d)^2
for small oscillations.