gob0b
- 2
- 0
Homework Statement
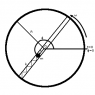
A massless wire hoop of radius R is rotating in a horizontal plane about its central point with constant velocity ω. There is a tube of negligible mass pinned across the hoop on a line passing through the central point. Inside this tube is a spring of negligible mass with spring co-efficient k, pinned at one end to the hoop, and at the other end to a mass m. The mass, spring, and tube experience no friction w.r.t. each other. (The mass is free to move within the confines of the tube, and is of the same width as the tube) Find the Lagrangian equations of motion for the mass, and describe under which conditions the mass will or will not oscillate.
Homework Equations
##\mathcal{L}=T-U##
##T=\frac{1}{2}mv^2##
##U=\frac{1}{2}k?^2## ?
The Attempt at a Solution
I was able to work out what I think is the correct description of the kinetic energy, T, but I am having some difficulty figuring out how to define the potential energy. I know that I need to work in absolute coordinates in order to use the Lagrange equations, and I chose to use 2D polar coordinates in ##(r,\phi)## with the origin at the center point of the hoop, giving ##T=\frac{1}{2}m\left(\dot{r}^2 + r^2\dot{\phi}^2\right)##. The distance r being measured from the center of the hoop it seemed to me that the potential energy should be ##U=\frac{1}{2}k\left(r+R-L\right)^2## with L being the rest length of the spring and R the radius of the hoop. My question am I on the right track? I hate filling a page with derivatives when I started out with the wrong assumptions.