kkcolwell
- 3
- 0
Homework Statement
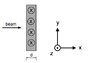
A beam of electrons is fired into a rectangular region of space that contains a uniform magnetic field in the -z direction. The electrons are moving in the +x direction, as shown. The speed of the electrons in the beam is 6.00 × 106 m/s. The mass of an electron is me = 9.11 × 10−31 kg. The magnitude of the magnetic field in the rectangular region of space is 1.50 × 10−2 T. The rectangular region has a width d.
What is the maximum value of d for which the electron beam will make it through to the other side of this rectangular region, and continue on to the right of the region?
Homework Equations
|⃗v|=|E⃗|/|B⃗1|
(Equations provided)
|F⃗m| = |q||⃗v||B⃗ || sin(θ)|
|F⃗m| = IL|B⃗ || sin θ| r = m | ⃗v |
|q||B⃗ | r = m | ⃗v ⊥ | |q||B⃗ |
|F⃗E|=|F⃗B| −→ q|E⃗|=q|⃗v||B⃗1| −→ |⃗v|=|E⃗|/|B⃗1| | m⃗ | = N I A
τ = NIA|B⃗||sinθ| = |m⃗ ||B⃗||sinθ|
| B⃗ | = μ 0 I 2πr
| B⃗ | = μ 0 N I 2r
| B⃗ | = μ 0 N I L
Φv =|⃗v|Acos(θ)
ΦB =|B⃗|Acos(θ)
E = N|∆Φ| ∆t
I = V/R
I = E/R (linear DC generator)
E = BvL (linear DC generator)
I = E/R = BvL/R (linear DC generator)
Fm = ILB = (B2vL2)/R (linear DC generator)
Pmechanical = Fappl v Pelectrical = IV = IE
ΦB = BA cos(ωt) (rotary AC generator)
E = (NBAω)sin(ωt) (rotary AC generator)
I = E/R = (NBAω/R) sin(ωt) 1Tesla(1T)=1 N
μ0 =4π×10−7 Tm A
The Attempt at a Solution
E=6.00 x 10^6m/s x 1.50 x 10^-2 T
90000 T x m/s
Ok the problem I am having is relating distance to any equation I have. In previous problems I have worked, none of them had distance as part of the problem. If someone could just give me a hint or something about how to relate distance to the problem, that would be much appreciated.
Attachments
Last edited: