Maximizing Energy Levels: Calculating Electron Transitions and Photon Momentum

[beibixx]

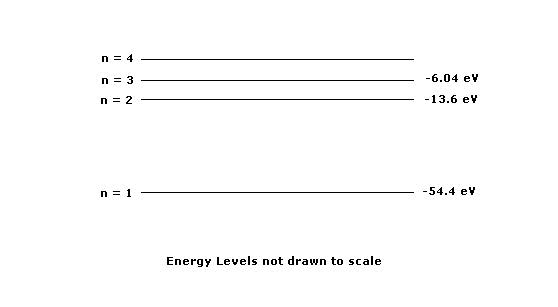
1. The diagram above shows the lowest four descrete energy levels of an atom. An electron in the n=4 state makes a transition to the n=2 state, emitting a photon of wavelength 121.9 nm

(a)Calculate the energy level of the n=4 state.
(b)Calbulate the momentum of the photon.

The photon is then incident on a silver surface in a photoelectric experiment, and the surface emits an electron with maximum possible kinetic energy. The work function of the silver is 4.7eV

(c) Calculate the kinetic energy, in eV, of the emitted electron.

2. E=hf
E= pc
h=6.63 x 10^-34J.s
h=4.14 x 10^-15eVs
KEmax = hf-work function
work function = hf0
v=fλ
λ=h/p3. ...might come back with this..

 

[buffordboy23]

(a)Calculate the energy level of the n=4 state.

Hi beibixx, welcome to PF.

For question (a), do you know what energy levels even are? If I asked you for the given diagram, what is the energy of a photon emitted due to an electron jumping from the n = 2 to the n = 1 state, would you know? For this problem, you are given the wavelength of the emitted photon, so how can you apply the previous question I asked to solve your problem?

 

[beibixx]

Thanks for the welcome! So after doing this I read the "energy levels not drawn to scale" and have a feeling that my assumption was wrong, but hey, you never know...

so
a)

For T1: Transition -54.4-(-13.6) = 40.8 eV
For T2: -13.6 - (-6.04) = 7.56 eV
T3=?
n4 = n3
so
-6.04 + 7.56 = 1.52 eV
T3 = 1.52 eV
n4 = 1.52 eV

b)
E = pc
c = 6.63 x 10^-34 JS
p = E/c
p = 1.52/ 6.63 x 10^-34 JS
p=2.29 x 10^33

c)
KEmax = hf - wo
wo = hf , given wo = 4.7 eV
E = hf , given h = 4.14 x 10^-15 eV

f = E/h
f = (1.52)/(4.14 x 10^-15)
f = 3.67 x 10^14 Hz

KEmax = (4.14 x 10^-15) (3.67 x 10^14) - 4.7eV
KEmax = 1.519 - 4.7
KEmax = -3.18062 ... okay.. doesn't make sense?

 

[beibixx]

I'm guessing this is wrong..

 

[beibixx]

sorry I re posted this and thought I could delete the old post but I have no idea how to do it...

 

[buffordboy23]

For T1: Transition -54.4-(-13.6) = 40.8 eV
For T2: -13.6 - (-6.04) = 7.56 eV
T3=?
n4 = n3
so
-6.04 + 7.56 = 1.52 eV
T3 = 1.52 eV
n4 = 1.52 eV

T1 and T2 are correct, but T3 is not. In fact, you calculated T3 in a completely different manner. For T1 and T2, you used the following equation:

E_{\gamma}=E_{m}-E_{n}

where m and n are energy level indexes such that m > n. This equation says that the energy of the photon is equal to the difference between the two energy levels. Now for your current problem you are not given E_{4}, but you are given \lambda_{42}, the wavelength of the photon from the n = 4 state to the n = 2 state. How can you use the wavelength to determine the energy of the photon for this transition? After you determine this, you can solve for E_{4}.

E = pc
c = 6.63 x 10^-34 JS
p = E/c
p = 1.52/ 6.63 x 10^-34 JS
p=2.29 x 10^33

Correct approach, but wrong answer since your answer in part a) is wrong.

KEmax = hf - wo
wo = hf , given wo = 4.7 eV
E = hf , given h = 4.14 x 10^-15 eV

f = E/h
f = (1.52)/(4.14 x 10^-15)
f = 3.67 x 10^14 Hz

KEmax = (4.14 x 10^-15) (3.67 x 10^14) - 4.7eV
KEmax = 1.519 - 4.7
KEmax = -3.18062 ... okay.. doesn't make sense?

There is no reason to calculate the frequency here. Remember the energy of the photon is E = hf, so use your answer from part a) in place of the hf.

NOTE: I used latex fonts for some equations here, but on my screen I see equations that I used from previous posts. Let me know if things look just as goofy on your end.

 

[beibixx]

Right..so to do this again.

For part a)
In order to find the energy level I use the equation E = (hc/lambda), with the given wavelength being 121.9nm and hc = 1.24 x 10^3eV*nm
So E = [(121.9nm)/1.24 x 10^3eV*nm)]
E=10.1723

For part b)
E=pc, where p is momentum
Rearranging this I find that p=(E/c)
where c approximately equals 3 x 10^17
so p=(10.173/3 x 10^17)
p=3.39 x 10^-17

For part c)
work function of silver is given as 4.7eV
KEmax=hf-work function
E= hf=pc
so replace hf with E
getting KEmax = E-work function
KEmax = 10.1723 - 4.7
KEmax=5.4723

 

[buffordboy23]

Part a) is still wrong, but parts b) and c) are correct in application (I didn't check for numerical accuracy) since they require the energy of the emitted photon.

In part a), you know the energy of the bounded electron-atom system associated with n = 2 but you do not know the energy for n = 4 (this is what you need to determine). Since you know the energy of the emitted photon, you can determine the energy of state n = 4 by a simple manipulation of the equation I gave you earlier:

E_photon = E_m - E_n

where m and n are indexes such m > n. In my first post, I asked you if you could determine the energy of the emitted photon (the unknown) for an electron transition from n = 2 to n = 1 using your diagram (E_2 and E_1 were the givens). Do you see the difference between the problem I gave you and the problem given to you by your professor? They are similar in the conceptual aspects, but the given data is different.

Here's a problem solving tip for part a) to know that your answer is wrong. Bounded electron-atom systems always have a negative energy associated with their energy levels; it's a general characteristic of bound systems. Since you obtained a positive answer, you must conclude that it is incorrect. Checking your final answers by knowing the quantitative constraints imposed by the conceptual aspects of the physics is an important problem-solving tool. Therefore, you should expect E_4 to have a higher energy than E_3 but less than 0; that is, -6.04 eV < E_4 < 0.