fiksx
- 77
- 1
- Homework Statement
- In a computer shop, there are $33$ PC set that are sold:
1. with 18 sets of PC have crystal screen PC included,
2. with 12 sets of PC have printer included,
3. with 6 sets of PC have scanner system included,
4. with 3 sets of PC that include all(printer, scanner system,
crystal screen pc)
- Relevant Equations
- x=33-(18-(a+b+3)+12-(a+c+3)+6-(b+c+3) + ( a+b+c +3 ) )
In a computer shop, there are $$33$$ PC set that are sold:
1. with 18 sets of PC have crystal screen PC included,
2. with 12 sets of PC have printer included,
3. with 6 sets of PC have scanner system included,
4. with 3 sets of PC that include all(printer, scanner system,
crystal screen pc)
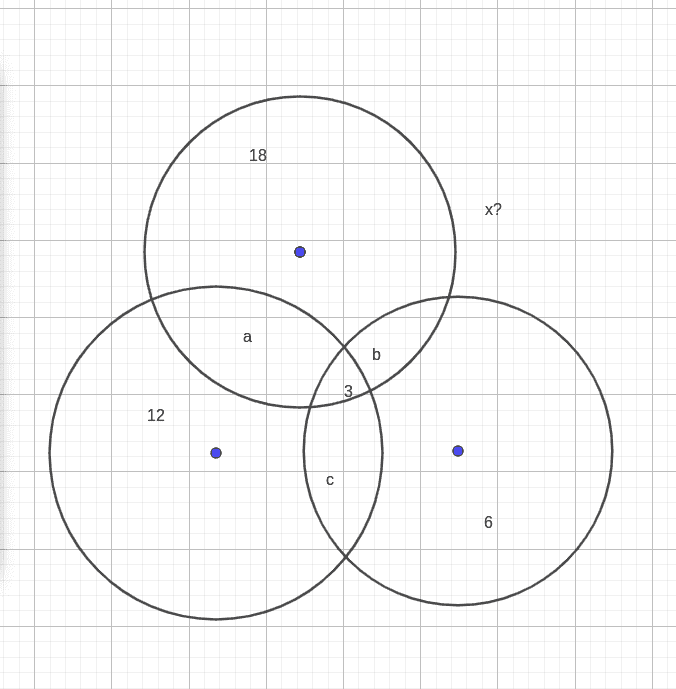 We want to find $$x$$ which is $$33-|S_1 \cup S_2 \cup S_3|=x$$ and get $$x$$ that is max
We want to find $$x$$ which is $$33-|S_1 \cup S_2 \cup S_3|=x$$ and get $$x$$ that is max
From the graph :
It means that inside $$18$$ crystal screen PC, there is a set that also includes a scanner or printer and, there is a set that contains only crystal screen.
1. ##S_1\implies 18=a+b+3+## crystal screen only
2. ##S_2\implies 12 = a+c+3+## printer only
3. ##S_3\implies 6=b+c +3+## scanner only
$$x=33-(18-(a+b+3)+12-(a+c+3)+6-(b+c+3) + ( a+b+c +3 ) )=x\\
33-(27-a-b-a-c-b-c + (a+b+c+3))=\\
33-(30 -a-b-c)=\\
3+a+b+c =x\\
a+b+c=x-3$$
More conclusions:
- $$a+c \le 9$$
- $$b+c \le 3$$
- $$a+b \le 15$$
What is the relation with $$x$$ and how do I get the actual result?
1. with 18 sets of PC have crystal screen PC included,
2. with 12 sets of PC have printer included,
3. with 6 sets of PC have scanner system included,
4. with 3 sets of PC that include all(printer, scanner system,
crystal screen pc)
From the graph :
It means that inside $$18$$ crystal screen PC, there is a set that also includes a scanner or printer and, there is a set that contains only crystal screen.
1. ##S_1\implies 18=a+b+3+## crystal screen only
2. ##S_2\implies 12 = a+c+3+## printer only
3. ##S_3\implies 6=b+c +3+## scanner only
$$x=33-(18-(a+b+3)+12-(a+c+3)+6-(b+c+3) + ( a+b+c +3 ) )=x\\
33-(27-a-b-a-c-b-c + (a+b+c+3))=\\
33-(30 -a-b-c)=\\
3+a+b+c =x\\
a+b+c=x-3$$
More conclusions:
- $$a+c \le 9$$
- $$b+c \le 3$$
- $$a+b \le 15$$
What is the relation with $$x$$ and how do I get the actual result?
Last edited by a moderator: