Better WOrld
- 80
- 1
Homework Statement
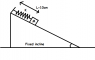
A block of mass ##M = 1 kg## is placed of a fixed rough incline of inclination
##\theta=sin^{-1} \frac{7}{10}## and coefficient of friction ##\mu=\frac{1}{\sqrt{51}}##. It is connected to a spring of spring constant 100 N/m. Initially the spring is in natural state with length = 10cm
If the block is left to move then find the final elongation in spring when block stops moving.
Take ##g= 10m/s^2##
Homework Equations
The Attempt at a Solution
The forces doing work on the block are gravity, the spring force, and friction. Initially, the velocity of the block is 0 and once the spring reaches its maximum extension, the velocity again becomes 0, hence the change in Kinetic Energy of the bock is 0. Let the maximum extension of the spring be ##X##.
\[\]
Applying the Work Energy Theorem,
$$W_{gravity}-W_{spring}-W_{friction}=\Delta K=0$$
$$mgX\sin\theta-\int_0^X kx dx-\mu mg\cos\theta X=0$$
$$mgX\sin(\sin^{-1}\dfrac{7}{10})-\dfrac{kX^2}{2}-\mu mg \cos(\sin^{-1}\dfrac{7}{10})=0$$
Putting in the given values,
$$7-50X-1=0$$
$$X=0.12m$$
However, this does not give the 'correct' answer - ##0.8m##. I would be truly grateful if somebody could please explain where I have gone wrong. Thanks in advance!