greg_rack
Gold Member
- 361
- 79
- Homework Statement
- A drawbridge system consists of a uniform ramp, of weight W , that is smoothly hinged at its lower end. The upper end is connected by a light, inextensible cable to a winch that is fixed to the wall in the position shown in the diagram(image below).
The ramp is lowered slowly, at constant speed, from its closed (vertical) position (θ = 0°) to its open (horizontal) position (θ = 90°).
What is the maximum tension in the cable during this process? (double-angle identities: sin 2θ = 2sin θ cos θ ; cos 2θ = cos2 θ – sin2 θ )
- Relevant Equations
- Weight
Trigonometry
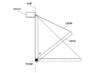
My result for this problem is correct, but I would like to submit to you the method I used since it doesn't convince me.
The problem asks for the maximum tension on the cable from the transition to 0 to 90 degrees; I firstly concluded just by thinking, not using formulas or particularly formal methods, that the maximum tension must have been exerted for Θ=90°. Consequently, I started writing down the free
body diagram, including the weight applied to the middle of the drawbridge and the cable tension applied to the right corner of the drawbridge.
Now, placing the total momentum Mtot=0, I found the final formula and the correct answer... but I have a question: why wouldn't it have worked by placing just the total forces Ftot=0? Is that a non-working condition in problems consisting of a rotating body around a pivot?
I'm sorry but its a lot of time that I'm not studying such topics... and sometimes I Get confused!