Mechanical Engineering 3D force system

[sami23]

Homework Statement

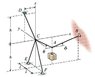
A system of cables suspends a crate weighing W = 420 lb. The dimensions in the figure are as follows: h = 20.9 ft, l = 5.70 ft, x = 7.05 ft, $$\theta$$ = 36.0$$\circ$$, and $$\phi$$ = 20.0$$\circ$$. Determine T_A, T_D, and T_E, the tensions in cable segments CA, CD, and CE, respectively.

Homework Equations

vector F = (magnitude F)(unit vector)
$$\sum$$F = 0
F_CA + F_CB + F_CD + F_CE + F_CF + W = 0

The Attempt at a Solution

How do I start by finding the coordinates:
C(0,0,0), D(x,0,h), A(?) E(?)

I can't see how to find the correct coordinates A,B,C,D,E,F

 

[pongo38]

Do you agree that A B C and D all lie in the xz plane?

 

[sami23]

yes they do. coordinates for D:(7.05,0,20.9)
C is at origin (0,0,0)
E and F are at some weird y plane (here's my attempt)
E: (x,l,-h)
F: (-x,-2l,-h)
A is all over the place with a weight

 

[pongo38]

It looks to me like E is at 0, l, -h and F is at 0, -l, -h
For the vagueness of A, you might realize that it's the angles that matter. The forces are independent of the actual distances. more dependant on distance ratios, that is angles. So to solve it you could say: Without loss of generality x of A=1 etc

 

[sami23]

I see how E(0,l,-h) and F(0,-l,-h). They're at the same y-plane just at opposite ends.
Now A makes those angles at the x-plane. AB forms phi and AC forms theta. All I really know about B is that it's in the -h z-plane. Can I treat A as a 2D problem in the xz-plane?

 

[pongo38]

Sloppy language when saying "They're at the same y-plane just at opposite ends", when you mean y-z plane. When you say "All I really know about B is that it's in the -h z-plane" I think you should say ...in the x-z plane.
When I said that WLOG, x of A can be set at unity, I implied that x of B can similarly be attributed a distance as long as it is bigger that x of A.
If you suppress the y-axis and look only at the x-z plane with E on top of F, you will get a meaningful result for DC CA and AB, but the result for C to EF will need to be partitioned in the y-z plane. That's the simple way to look at it. Or you could invoke vector algebra with i j k terms. If you start with the joint at A, you can solve the forces there. Then you have enough information to go to C, where you will need three equations for the three unknowns. That's where 3 reference axes are helpful to bring the question to a successful conclusion. Can you do it now?

 

[sami23]

thanks