davidgruty
- 20
- 0
Hello!
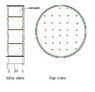
I have to calculate some pieces (brown "plugs" and green ring) which hold two plates of 2 mm each. They are made of an insulation material (different the green and the brown one) with known properties.
One plate is made of aluminium and the other of carbon fibre.
Inside the two plates there is vacuum.
The point is I want to hold the two plates keeping them flat (no dent) and calculate the number and dimension of the "plugs" (they have to be placed in a homogeneous way, the paint drawing is not very good...)
Can anyone help me?
The problem I have is the vacuum, I made some calculations with forces but never with vacuum.
Thank you very much.
Regards
I have to calculate some pieces (brown "plugs" and green ring) which hold two plates of 2 mm each. They are made of an insulation material (different the green and the brown one) with known properties.
One plate is made of aluminium and the other of carbon fibre.
Inside the two plates there is vacuum.
The point is I want to hold the two plates keeping them flat (no dent) and calculate the number and dimension of the "plugs" (they have to be placed in a homogeneous way, the paint drawing is not very good...)
Can anyone help me?
The problem I have is the vacuum, I made some calculations with forces but never with vacuum.
Thank you very much.
Regards