Mechanics of material: an Axial Load Problem

[dikimbi2]

Hey Guys, here is a skeleton for an exercise I need a help with:

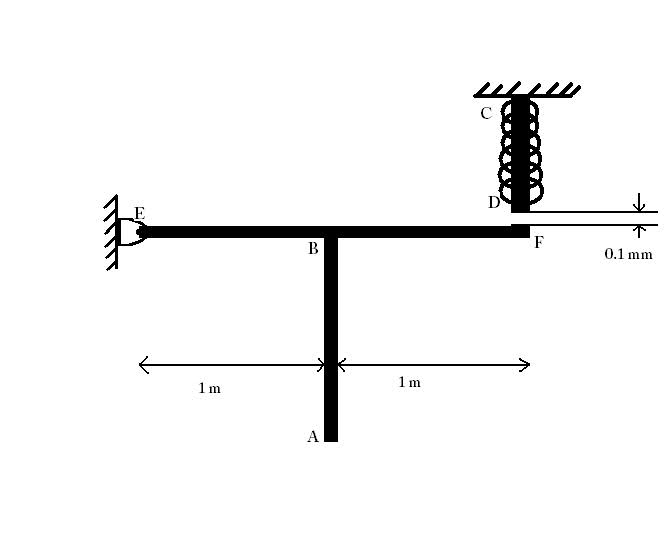
In this Problem we have a beam EF which is pin-supported at E, a Rod CD which is enrolled by a spring ( spring constant =k) and a rod AB (AB is touching the ground, I forgot to draw it).

If we heat the Rod AB what will be the equation of equilibrium and the compatibility equations to find the forces F_AB, F_CD and F_sp (the force of the spring).

(Gap between CD and EF is equal to 0.1 mm)

I just want to know the equations because I don't remember the rest of the numerical given.

Thanks everyone,
Dikimbi2.

 

[dikimbi2]

Again Hi, sorry I forgot to show you what I did: (I had this in an exam):

Equilibrium equation: (Moment about point E) M_E = 0 =>

F_AB = 2(F_CD+F_sp)

Compatibility equations: [(δ_AB)_t – (δ_AB)_F]/1 = [(δ_CD)_F]/2 (Using Thales)

(δ_AB)_t = α_al. ΔT.L_AB

(δ_AB)_F = (F_AB.L_AB)/(A_AB.E_AB)

(δ_CD)_F = (F_CD + F_sp) / (k_CD + k_sp)

with k_CD = (A_CD.E_CD)/(L_CD)

The Other Compatibility equation is: (δ'_CD)=(δ_sp)

δ'_CD = (F_CD)/(k_CD)
(δ_sp = (F_sp)/(k_sp)