Eugbug
- 21
- 0
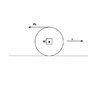
If an axle is being pulled with a tractive effort E, can this be resolved into a couple and forwards force E at the point of contact with a surface? Is it correct to add a limiting friction force F acting backwards against the direction of motion and if this is exceeded by E, does the wheel slip?