RioAlvarado
- 15
- 4
Homework Statement
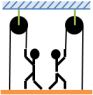
Two construction workers each of mass m raise themselves on a hanging platform using pulleys as shown above. If the platform has a mass of 1.2⋅m, the initial distance between the pulleys and the platform is d, and the workers each pull with a force f on the ropes, what is the acceleration a of the workers? Assume the pulleys and ropes are massless.[/B]
Homework Equations
Tension = m(a + g) (possibly).
F = ma[/B]
The Attempt at a Solution
To be wholly honest I have next to no idea how to proceed. My only real thought was to use F = ma. Thinking first that I'd need my total mass, I added (m + m + 1.2m) = 3.2m total (one mass for each worker plus the platform). Next I tried to consider the force, thinking we have two workers each exerting a tension force f, thus 2f being the total force upwards, then subtracting out the downward forces (namely gravity) to achieve (2f - 3.2mg). Plugging into F = ma I got (2f - 3.2mg) = a(3.2m) => a = (2f - 3.2mg)/(3.2m) which is marked incorrect. At this point I have hit a wall. My thanks for any help. (Attached is the image accompanying the problem). [/B]
Attachments
Last edited: