What is the viscous force acting on an oil drop in Millikan's experiment?

  • Thread starter Krushnaraj Pandya
  • Start date
  • Tags
    Drop Oil
In summary: See my later edit above.Oh, right- I got the correct answer by equating forces in vertical and horizontal directions and plugging into the first. My main mistake was that I considered F to be the same in both cases, Thank you very much for your help :D
  • #1
Krushnaraj Pandya
Gold Member
697
73

Homework Statement


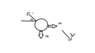
In Millikan's oil drop experiment on applying a vertically upward electric field an oil drop (of mass m) moves vertically downward with certain terminal speed. On applying double the electric field in horizontal direction, the drop moves making 45 degrees with the vertical. Neglecting buoyant force due to air, what is the viscous force acting on the drop in first case?

Homework Equations


Fluid mechanics+electrostatics+mechanics equations

The Attempt at a Solution


Attached below. From first case, qE+F(viscous force)=mg, from second case F/root2 =mg but this is inconsistent and the answer is mg/2. I'd be grateful for some help
firstcase.jpg
case2.png
 

Attachments

  • firstcase.jpg
    firstcase.jpg
    7.3 KB · Views: 533
  • case2.png
    case2.png
    4.1 KB · Views: 520
Physics news on Phys.org
  • #2
Without the horizontal field it was moving downwards. In your diagram, after adding a horizontal field you have it moving upwards. Does that seem reasonable?
 
  • #3
haruspex said:
Without the horizontal field it was moving downwards. In your diagram, after adding a horizontal field you have it moving upwards. Does that seem reasonable?
The arrow shows the viscous force, I have it moving downwards. Note the separate arrow pointing southeast shows the velocity.
 
  • #4
Krushnaraj Pandya said:
The arrow shows the viscous force, I have it moving downwards. Note the separate arrow pointing southeast shows the velocity.
Sorry, I should have read it more carefully.
Are you assuming the viscous force is the same in both cases?

In the second diagram, isn't the vertical electric force still acting?
However, to get the answer mg/2 I have to assume it is no longer acting.
What does the fact that it moves at 45 degrees tell you about the applied forces in the second case?
 
  • Like
Likes Krushnaraj Pandya
  • #5
haruspex said:
Sorry, I should have read it more carefully.
Are you assuming the viscous force is the same in both cases?
the viscous force is 6pi*r*n*v. I noticed just now that the velocity might be different in both cases. How can we obtain a relation between them?
 
  • #6
Krushnaraj Pandya said:
the viscous force is 6pi*r*n*v. I noticed just now that the velocity might be different in both cases. How can we obtain a relation between them?
See my later edit above.
 
  • #7
Oh, right- I got the correct answer by equating forces in vertical and horizontal directions and plugging into the first. My main mistake was that I considered F to be the same in both cases, Thank you very much for your help :D
 

1. What is Millikan's oil drop problem?

Millikan's oil drop problem, also known as the Millikan experiment, is a famous physics experiment conducted by Robert A. Millikan in 1909 to determine the charge of an electron.

2. How did Millikan solve the oil drop problem?

Millikan used a chamber filled with air to suspend tiny oil droplets and applied an electric field to measure the charge on each droplet. The droplets were then compared to the gravitational force acting on them, allowing Millikan to calculate the charge of an electron.

3. What was the significance of Millikan's oil drop experiment?

Millikan's experiment was a crucial step in understanding the nature of electrons and their charge. It also helped to determine the fundamental charge of an electron, which is a key value in many areas of physics and chemistry.

4. What challenges did Millikan face during the oil drop experiment?

One of the main challenges Millikan faced was controlling the size and charge of the oil droplets. He had to carefully select the oil and control the environmental factors, such as temperature and humidity, to ensure accurate results.

5. How did Millikan's oil drop experiment contribute to the development of modern physics?

Millikan's experiment provided evidence for the quantization of electric charge, which led to the development of quantum mechanics and the understanding of subatomic particles. It also paved the way for further research into the nature of electrons and their role in electricity and magnetism.

Similar threads

Calculating Velocity in the Millikan Oil Drop Experiment
    • Introductory Physics Homework Help
2
Replies
52
Views
3K
Calculating Charge of an Electron w/ the Millikan Oil Drop Experiment
    • Introductory Physics Homework Help
Replies
12
Views
1K
Millikan Oil drop lab experiment - equation for speed of drop
    • Introductory Physics Homework Help
Replies
3
Views
1K
Millikan's Oil-Drop Experiment: Is my reasoning correct?
    • Introductory Physics Homework Help
Replies
1
Views
1K
Calculating Charge Of Electron (Millikan Oil Drop Experiment
    • Introductory Physics Homework Help
Replies
1
Views
2K
Charge on plates in Millikan's Experiment
    • Introductory Physics Homework Help
Replies
5
Views
2K
Millikan oil drop experiment
    • Introductory Physics Homework Help
Replies
2
Views
2K
What is the charge of the oil drop in Millikan's experiment?
    • Introductory Physics Homework Help
Replies
10
Views
5K
Millikan oil drop experiment charge determination
    • Introductory Physics Homework Help
Replies
6
Views
2K
Millikan's oil drop experiment direction
    • Introductory Physics Homework Help
Replies
4
Views
3K

Hot Threads

Recent Insights

Back
Top