Minimum Impact Velocity for Pendulum to Swing Over Top of Arc

[gregcor]

Homework Statement

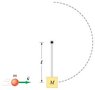
A pendulum consists of a mass M hanging at the bottom end of a massless rod of length l, which has a frictionless pivot at its top end. A mass m, moving as shown in the figure with velocity v impacts M and becomes embedded.

What is the smallest value of v sufficient to cause the pendulum (with embedded mass m) to swing clear over the top of its arc?

Homework Equations

$$p=mv$$

The Attempt at a Solution

I realize that the acceleration must be $$\frac{v^2}{l}=g$$ to swing over the arc. Thus, I found:

$$v_f=mv_i/(m+M)$$, and set V_f equal to $$\sqrt{lg}$$ from the first equation.

I got:
$$v_i=\frac{(m+M)\sqrt{lg}}{m}$$

But the software returned:

Your answer either contains an incorrect numerical multiplier or is missing one.

Help!
Thanks!

 

[LowlyPion]

What is the top of its arc?

Is there a figure you can provide or describe in better detail?

 

[gregcor]

What is the top of its arc?

Is there a figure you can provide or describe in better detail?

Sure. See the attachment.
Thanks!