qlzlahs
- 13
- 0
Homework Statement
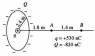
A charge Q = -820 nC is uniformly distributed on a ring of 2.4 m radius. A point charge q = +530 nC is fixed at the center of the ring. Points A and B are located on the axis of the ring, as shown in the figure. What is the minimum work that an external force must do to transport an electron from B to A?
(e = 1.60 × 10^-19 C, k = 1/4πε_0 = 8.99 × 10^9 N · m^2/C^2)
https://www.physicsforums.com/attachments/work-png.93021/?temp_hash=3fc763fb95a2d9ab71f3bf4a54a23c14
Homework Equations
V = (k*q)/(sqrt(R^2 + z^2))
work = (V_b - V_a)*q
work = (k*q_1*q_2)/r
The Attempt at a Solution
V_B = (9*10^9*530*10^(-9))/(3.2) = 1490.625 V
V_A = (9*10^9*530*10^(-9))/(1.8) = 2650 V
V_B - V_A = -1159.375 V
(V_B - V_A)*q, where q = 1.60*10^-19 C
(-1159.375)*(1.60*10^-19) = -1.855*10^-16 J
I'm not sure if I'm supposed to use -820 nC or 530 nC for the q value when calculating V_B or V_A.