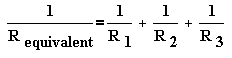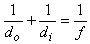Mirror/Lens Equation and Resistors in Parallel

[jefgreen]

I'm not sure how to find the least common denominator when given these formulas:

 

[jefgreen]

In addition, sometimes I am asked to solve for R2 (using the Parallel circuits equation) and do (using the mirror/lens equation).

 

[jefgreen]

Bump10char.

 

[cartonn30gel]

Do you have an example with numbers in it? How about (1/9)+(1/4)+(1/12)?
Try to do that and show your work and where you're stuck. If you have a better example, feel free to show your work with that one.

 

[cartonn30gel]

Do you have an example with numbers in it? How about (1/9)+(1/4)+(1/12)?
Try to do that and show your work and where you're stuck. If you have a better example, feel free to show your work with that one.

 

[jefgreen]

36 would be the lowest common denominator.

1/36+1/36+1/36=3/36?

36/3=12

Correct?

 

[jefgreen]

Bump10char

 

[Daft]

The LCM is 36, but its not 1/36+1/36+1/36

is 1/9 = 1/36?
is 1/4 = 1/36?
is 1/12 = 1/36?

 

[jefgreen]

The LCM is 36, but its not 1/36+1/36+1/36

is 1/9 = 1/36?
is 1/4 = 1/36?
is 1/12 = 1/36?

I apologize for my pathetic lack of basic math, but could you walk me through the process of how to get the answer?

 

[Daft]

Okay, look at this this way (I really don't mean to sound condescending, so sorry if it does):

2/4 = 1/2 right? That's easy to understand

We have to add:

1/9 + 1/4 + 1/12

What we have to do is write these fractions in a way that they all have the same denominator (which is the lcm, 36)

So the value of the fractions stay the same, we just write them in a different way

Let's use 1/9:

In the same way that 2/4 = 1/2,

1/9 = some number / 36. All you have to do is ask yourself, what number to I multiply by 9 to get 36? The answer is 4

therefore: 1/9 = 4/36

Do the same for 1/4. What multiplied by 4 = 36? the answer is 9

so 1/4 = 9/36

What multiplied by 12 = 36?

So 1/12 =

Spoiler

3/36

Then you just write them like that (with the same denominator) and add them, and you have your answer.

You said you sometimes have to solve for R2 or d0. For these you can just rearrage the equations

eg: from 1/Re = 1/R1 + 1/R2 + 1/R3 (the 'e' means equivalent) you get

1/R2 = 1/Re - 1/R1 - 1/R2

The same can be done for d0

 

[collinsmark]

Here is some general advice. I'll start simple, with basic fractions.

Useful rule (1). If you multiply the denominator by some number, and you multiply the numerator by the same number, it doesn't change the fraction. Here is an example. Suppose you have some fraction, such as

$$\frac{3}{4}$$

then if we multiply both the numerator and denominator by 5, the fraction is the same as it was before:

$$\frac{3(5)}{4(5)} = \frac{15}{20}$$

What that means is 3/4 and 15/20 are the same number! The same works for dividing. If we divide both the numerator and denominator by the same number, it doesn't change the fraction.

$$\frac{15}{20} = \frac{\frac{15}{5}}{\frac{20}{5}} = \frac{3}{4}$$

The same does not apply to addition or subtraction. It only works for multiplication and division. So don't add or subtract some constant from both the numerator and denominator; it will change the value of the fraction!

Useful rule (2). You can add the numerators of fractions together if they share a common denominator. Here is an example.

$$\frac{1}{10} + \frac{3}{10} = \frac{4}{10}$$

Now let's combine ideas 1 and 2 together in an example.

$$\frac{1}{2} - \frac{1}{3} + \frac{3}{4}$$

The first thing to do is find a common denominator. In this case it is 12.

$$= \frac{1(6)}{2(6)} - \frac{1(4)}{3(4)} + \frac{3(3)}{4(3)}$$

$$= \frac{6}{12} - \frac{4}{12} + \frac{9}{12}$$

$$= \frac{6 - 4 + 9}{12}$$

$$= \frac{11}{12}$$

Useful rule (3). If you are trying to find a common denominator, and can't come up with a simple one, you can always multiply the denominators together as a sure thing. Here is an example:

$$\frac{1}{11} + \frac{3}{13} = \frac{1(13)}{11(13)} + \frac{3(11)}{13(11)} = \frac{13 + 33}{143} = \frac{46}{143}$$

Useful rule (4). The same works for variables. Consider the example,

$$\frac{1}{10} + \frac{1}{R}$$

$$= \frac{1(R)}{10(R)} + \frac{1(10)}{R(10)}$$

$$= \frac{R + 10}{10R}$$

=========== Now let's consider a more complicated example.

Suppose we have

$$\frac{1}{R_{eq}} = \frac{1}{R} + \frac{1}{20}$$

And the goal is to solve for R, in terms of R_eq.

Let's start by putting the terms with R in them on one side of the equation.

$$\frac{1}{R} = \frac{1}{R_{eq}} - \frac{1}{20}$$

Find a common denominator for the right side.

$$\frac{1}{R} = \frac{1(20)}{R_{eq}(20)} - \frac{1(R_{eq})}{20(R_{eq})}$$

Simplify,

$$\frac{1}{R} = \frac{20}{20R_{eq}} - \frac{R_{eq}}{20R_{eq}}$$

which becomes,

$$\frac{1}{R} = \frac{20 - R_{eq}}{20R_{eq}}$$

Invert both sides of the equation,

$$R = \frac{1}{\frac{20 - R_{eq}}{20R_{eq}}}$$

Thus,

$$R = \frac{20R_{eq}}{20 - R_{eq}}$$

Does that make any more sense?

 

[jefgreen]

Thank you guys for all of the help. I understand everything :).