CAF123
Gold Member
- 2,918
- 87
Homework Statement
A thunder cloud can be loosely modeled by two point charges -q and q at heights h and d above the Earth's surface with d > h. Model the Earth's surface as a conducting plane at z=0.
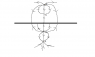
Sketch the Electric field lines (on a plane perpendicular to the earth). Indicate the field below the cloud, at a radial distance r, and far away from the cloud. Considering ##\underline{E}##, where is the safest place to be?
The Attempt at a Solution
To satisfy the boundary conditions (V=0 on surface of earth), two image charges are placed at a distance -h (a +q charge) and -d(a -q charge) from the plane. I have the potential due to all 4 charges as a function of x,y and z, from which I found the electric field as a function of the same variables.
From looking at the sketch, it appears to me that the E field should point in the +ve z direction below the cloud and this is confirmed by my eqn for E.
My expression for V is $$V=\frac{q}{4\pi\epsilon_o}\left(\frac{1}{(x^2+y^2+(z-d)^2)^{1/2}} - \frac{1}{(x^2+y^2+(z-h)^2)^{1/2}} - \frac{1}{(x^2+y^2+(z+d)^2)^{1/2}} + \frac{1}{(x^2+y^2+(z+h)^2)^{1/2}}\right)$$ and I found E by doing -gradV. (the expression is messier than the potential so I won't post it).. I can draw the general sketch of the field lines emanating form the dipole, but I am not sure if that is what the question requires. Perhaps it wants me to draw the general sketch and then confirm it with my eqn for E at particular points.
The safest place would be the place where E vanishes on the surface, but I am not sure how to express this in words or mathematically. I set ##E_z(x,y)=0## and I obtained a condition on ##r^2 = x^2 + y^2##.
I attached a sketch of my drawing
Many thanks.
Attachments
Last edited: