zwingtip
- 20
- 0
Homework Statement
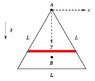
[PLAIN]http://img59.imageshack.us/img59/9484/fp5.gif
to find the moment of inertia through point A
Homework Equations
I = \int{r^2dm}
The Attempt at a Solution
Used a double integral from point A:
<br /> \displaystyle\int_{0}^{h}\displaystyle\int_{-L/2}^{L/2}\rho(x^2+y^2)dxdy<br /> = \rho\displaystyle\int_{0}^{h}\(\frac{1}{12}L^3+Ly^2)dy = \rho(\frac{1}{12}L^3h+\frac{1}{3}Lh^3)<br />
with
h=\frac{\sqrt{3}}{2}L
and
\rho=\frac{M}{\frac{1}{2}Lh}
and ended up with I = \frac{2}{3}ML^2
This seems too simple to be right. Help?
Last edited by a moderator: