Karol
- 1,380
- 22
Homework Statement
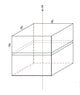
Calculate the moment of inertia of a cube of mass M and edges d round an axiz, z, that passes in the middle.
Then calculate around an axis parallel to the z axis and passing on one of the edges
Homework Equations
Moment of inertia: ##I=\int r^2dm##
The Attempt at a Solution
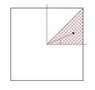
I slice the cube into rectangular slices of thickness dz. i sum infinitesimal masses dm along the radius till it reaches the edge. this way i get I for a triangle. there are 8 like these.
The radius's length, from the center to the edge is ##r=\frac{d}{2\cos\theta}##
The infinitesimal mass is ##dm=\frac{M}{d^3}dr^2 dz##
$$I=\frac{8M}{d^3} \int_{z=-\frac{d}{2}}^{z=\frac{d}{2}} dz \int_{\theta=0}^{\theta=\frac{\pi}{4}} d\theta \int_{r=0}^{r=\frac{d}{2\cos\theta}} r^2 dr =\frac{8M}{3d^3} \int_{z=-\frac{d}{2}}^{z=\frac{d}{2}} dz \int_{\theta=0}^{\theta=\frac{\pi}{4}} d\theta (r^3)\vert_0^{\frac{d}{2\cos\theta}}$$
$$I=\frac{M}{3}\int _{z=-\frac{d}{2}}^{z=\frac{d}{2}} dz \int_{\theta=0}^{\theta=\frac{\pi}{4}} \frac{1}{\cos^3\theta} d\theta$$
$$\int \sec^3 x=\frac{1}{2} (\sec x \tan x+\ln |\sec x +\tan x|)$$
$$\int_{\theta=0}^{\theta=\frac{\pi}{4}} \frac{1}{\cos^3\theta} d\theta=\frac{1}{2} (\sec \theta \tan \theta+\ln |\sec \theta +\tan \theta|)\vert_0^{\frac{\pi}{4}}=\frac{1}{2} (\sqrt{2}+\ln(\sqrt{2}+1)-\ln 1)=2.29$$
It's incorrect