Adam@Home
- 2
- 0
Hi all, I've been here before out of geneal interest but this is my first post, so i hope it's in the right spot.
I have a problem that I need an answer to, unfortunately due to sickness i wasn't at school when we were taught the theory of moments (called torque by some).
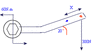
Anyway my question: I have to replace the force shown in the diagram (below or at the URL below) with a single force at the blue dot (x meters away from the 300N force). It said as a hint we should calculate x first.
Ok, I have NO IDEA how to do this. Any help or just a push in the right direction would be much appreciated.
Thanks in advance
Adam
URL of pic: http://www.geocities.com/gambleonlinecasino/question.gif http://www.geocities.com/gambleonlinecasino/question.gif
I have a problem that I need an answer to, unfortunately due to sickness i wasn't at school when we were taught the theory of moments (called torque by some).
Anyway my question: I have to replace the force shown in the diagram (below or at the URL below) with a single force at the blue dot (x meters away from the 300N force). It said as a hint we should calculate x first.
Ok, I have NO IDEA how to do this. Any help or just a push in the right direction would be much appreciated.
Thanks in advance
Adam
URL of pic: http://www.geocities.com/gambleonlinecasino/question.gif http://www.geocities.com/gambleonlinecasino/question.gif