Beamsbox
- 61
- 0
Calculus based course, this is from the "linear momentum of a system of particles" section.
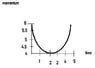
I've attached a rough sketch of the graph from my textbook. The main points of the graph are this, it's a parabola, at T=0 and T = 4.5, P(momentum) = 6. At T= 2.25 (maybe) it bottoms out. I say maybe because it doesn't really say where exactly it bottoms out, just shows a graph... and it appears to bottom out between 2 and 2.5.
The question:
At Time t = 0, a ball is struck at ground level and sent over level ground. (The graph) gives the magnitude (p) of the ball's momentum versus time (t) during the flight. At what angle is the ball launched?
Possibly useful equations (just not sure which to use):
Pi = Pf = mivi = mfvf(conservation of momentum)
Fnet = dp/dt
P = Mvcom (com meaning the com)
My thoughts:
Not sure where to start, other than taking the derivative of the momentum, but I'm not sure how to find the equation of the parabola... I've come close, but even if I had it, thus converting it to the force, I'm not sure where the angle would come in... though I thinkif I could get to that point I could figure it out.
Thanks prior, all.
I've attached a rough sketch of the graph from my textbook. The main points of the graph are this, it's a parabola, at T=0 and T = 4.5, P(momentum) = 6. At T= 2.25 (maybe) it bottoms out. I say maybe because it doesn't really say where exactly it bottoms out, just shows a graph... and it appears to bottom out between 2 and 2.5.
The question:
At Time t = 0, a ball is struck at ground level and sent over level ground. (The graph) gives the magnitude (p) of the ball's momentum versus time (t) during the flight. At what angle is the ball launched?
Possibly useful equations (just not sure which to use):
Pi = Pf = mivi = mfvf(conservation of momentum)
Fnet = dp/dt
P = Mvcom (com meaning the com)
My thoughts:
Not sure where to start, other than taking the derivative of the momentum, but I'm not sure how to find the equation of the parabola... I've come close, but even if I had it, thus converting it to the force, I'm not sure where the angle would come in... though I thinkif I could get to that point I could figure it out.
Thanks prior, all.