al_9591
- 12
- 0
Dynamics. Motion of 3 bodies
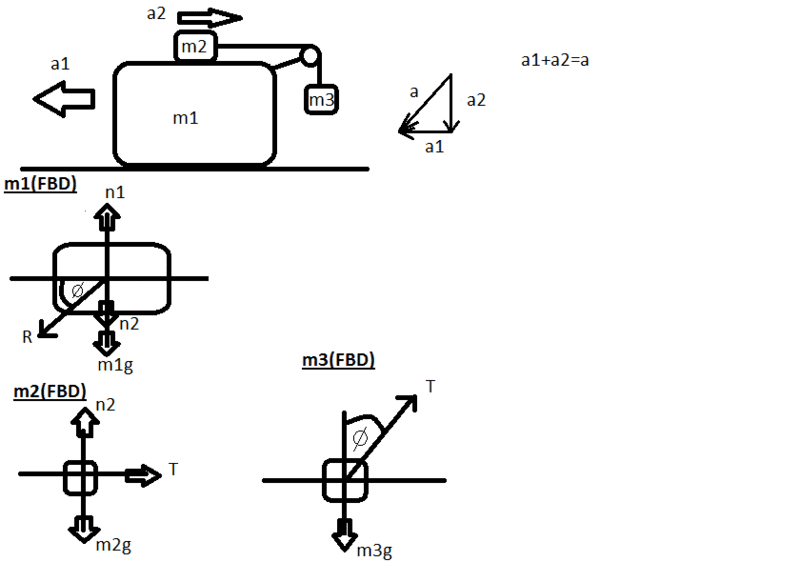
Initially the system of masses is held
motionless. All surfaces, and pulley are frictionless.
At the instant after the system of objects is released,
find the accelerations of m1, m2 and m3.
Data:
m1, m2 and m3
F=ma
EQUATIONS
FBD(free body diagram) of m1
X: Rcos(theta)=a1m1
Y: n1=n2+m1g
FBD of m2
X: T=(a2-a1)m2
Y: n2=m2g
FBD of m3
X: Tsin(theta)=a1
Y: Tcos(theta)-m3g=a2
This is what I have done so far are my equations correct?
Should I include the force n2 (normal 2) in the equation for the Y axis for mass 1?
Homework Statement
Initially the system of masses is held
motionless. All surfaces, and pulley are frictionless.
At the instant after the system of objects is released,
find the accelerations of m1, m2 and m3.
Data:
m1, m2 and m3
Homework Equations
F=ma
The Attempt at a Solution
EQUATIONS
FBD(free body diagram) of m1
X: Rcos(theta)=a1m1
Y: n1=n2+m1g
FBD of m2
X: T=(a2-a1)m2
Y: n2=m2g
FBD of m3
X: Tsin(theta)=a1
Y: Tcos(theta)-m3g=a2
This is what I have done so far are my equations correct?
Should I include the force n2 (normal 2) in the equation for the Y axis for mass 1?
Attachments
Last edited: