ChessEnthusiast
- 115
- 3
Homework Statement
An electron is shot towards an infinitely long wire with high current flowing througuh it.
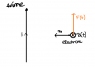
Please, look at my "sketch" in the attachment.
How will its trajectory be affected? What curve will it be?
2. The attempt at a solution
I thought about circular motion, but the fact that force changes rather rules that out.
What about an ellipse?