Motor in a pulley system with weight help (Sort of a dynamics problem)

[emzee1]

Homework Statement

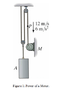
At the instant shown, point P on the cable has a velocity 12 m/s, which is
increasing at the rate of 6m/s^2. Determine the power input of motor M at this
instant if it operates with an efficiency of 0.8. The mass of the block A is 50kg. I've attached a picture of the problem.

Homework Equations

F=ma
Power = F*v (F=force, v=velocity)

The Attempt at a Solution

All I did was make an attempt at drawing free-body diagrams. For the block A of 50kg, I did:

2T-mg=ma; 2T-50(g)=50(6); T= 395 N

Then for point P, I assumed 395 = force of the motor, and thus:
395(12)= 4,740
Input Power = (4,740/.8) = 5,925 W

This is wrong obviously, and was hoping if someone could help me out on where I'm going wrong.

 

[TSny]

Think a bit more about the acceleration of block A. Are you sure it's the same as the acceleration of point P?

 

[emzee1]

Well, reviewing some previous examples, it doesn't. How do I go about solving for the acceleration for block A, and does it matter for the overall problem? Because I can't solve the following equation:

2T-mg = ma; as I do not know T nor a
and I'm not entirely positive about the free-body diagram at point P other than Force of motor pointing downwards, and Tension pointing upwards (i.e what does that equal to?).

 

[azizlwl]

deleting my post.

 

[TSny]

You can get the acceleration of block A in terms of the acceleration of point P. First consider displacements. If point P moves 1 m down, how far does block A go up?
[P.S. You won't need a free-body diagram for point P. You already have the correct equation for block A: 2T-mg = ma.]

 

[emzee1]

Let me try.

W=Fv
F-mg/2=ma
W=(ma+mg/2)v.

That is incorrect unfortunately. I've tried that also. The answer given is that the Power input should be 4803.75 W.

Solving your way does not give that answer (.8 = Power_input/Power_output).

 

[TSny]

Once you get the correct acceleration for block A, you will get the correct answer by repeating your original calculation.

 

[emzee1]

I'm really bad with multiple pulley-systems. Because there are 2 pulleys, is the acceleration just for block A just 1/2 of that at point P?

 

[azizlwl]

That is incorrect unfortunately. I've tried that also. The answer given is that the Power input should be 4803.75 W.

Solving your way does not give that answer (.8 = Power_input/Power_output).

Yes I've done it wrongly by taking point P as reference.

 

[TSny]

Yes, block A has 1/2 the acceleration of P. Try to imagine what would happen if you used your hand to lift block A and its pulley by 0.5 m. That would leave 1.0 m of slack in the string due to there being string on both sides of the pulley connected to A. So, point P would need to travel 1.0 m down to take out the slack. So, P always moves twice as far as A. Thus P is always moving twice as fast as A. Hence, during any time interval, the change in speed of P is always twice the change in speed of A. Therefore, the acceleration of P is twice the acceleration of A.

 

[emzee1]

So the acceleration of block A would be 3 m/s^2 ?

Putting this into the equation: 2T-mg=ma; where m=50kg and a = 3m/s^2, solving for T gets me 320 N.

P_input = 320(12), and solving for P_ouput; ((320(12)/.8)=4800W.

Did I do everything correctly? Because the answer given is 4,803.75W...

 

[TSny]

Try g = 9.81 m/s^2 rather than 9.8

 

[emzee1]

Try g = 9.81 m/s^2 rather than 9.8

Thank you so very much! Cleared up a lot of confusion for me!

 

[TSny]

Good work, emzee1.