GregoryGr
- 41
- 0
Homework Statement
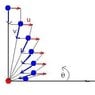
A boy is on a boat, at a distance H from the shore, when he sees a girl (at the point on the shore where the distance is measured) running with a constant velocity u parallel to the shore. At that time, he moves towards her, with a speed v, in such a way, that the point of the boat is always pointed at the girl (so his vector is always pointing her way). Find the time of their meeting.
Homework Equations
$$ \vec{v}= \frac{dr}{dt}\hat{r}+r\frac{d\theta}{dt}\hat{\theta} $$
The Attempt at a Solution
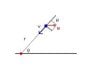
I changed the system of coordinates so the girl is stationary at O' , and using polar coordinates since the vector of the boat is always in the radial direction. The velocity for the boat in polar coordinates can be written:
$$ \vec{v}= -(v+ucos\theta)\hat{r}+vsin\theta\hat{\theta} $$
And since the 2 quantities in front of the singular vectors must be the same, I get 2 differential equations which give me this:
$$ \frac{dr}{r}= \frac{-(v-ucos\theta)d\theta}{usin\theta} $$
I am a noob at solving differentials, so firstly, are my equations right, and second, can somebody help me figure out how to do the math?