Multivariable Calculus, inspection of (0,0) for f(x,y) = y^2+3x^4-4yx^2

[shanu_bhaiya]

The Problem:
Problem is reference to Problem 23 on Page 210 of Basic Multivariable Calculus by Marsden, Tromba, Weinstein. But my problem is a bit different.

The main problem is:
For the function f(x,y) = y²+3x⁴-4x²y , is (0,0) a local maxima, minima or saddle point?

The secondary problem is that after the failure of method 1, the methods 2 and 3 contradict and method 4 supports method 3.

I approach the problem via different methods given below, some of which prove that (0,0) is a minima and others prove that it is maxima.

The Attempt at a Solution:

We investigate the function f(x,y) = y²+3x⁴-4x²y and its critical point (0,0):

f_x = -8xy+12x³
f_y = -4x²+2y
Hence, f_x = f_y = 0 implies:
Critical point or extremum is (0,0)
---------------------------------------------------------------------------------
METHOD 1:
Now, we check whether (0,0) is a maxima, a minima or a saddle point:
f_xx = -8y + 36x², hence f_xx(0,0) = 0
f_yy = 2, hence f_yy(0,0) = 2
f_xy = f_yx = -8x, hence f_xy(0,0) = 0

Now, we apply the second derivative test for maxima-minima:
f_xxf_yy – (f_xy)²
= 0 x 2 – 0 = 0.

Hence, second derivative test fails in this case.
---------------------------------------------------------------------------------
Hence, we think of an alternative method as following:
METHOD 2:
We put y = mx in the equation and then judge the function according to the one-variable calculus:

f(x,mx) = g(x) = m²x² + 3x⁴ – 4mx³
g’(x) = 2m²x + 12x³ – 12mx²
g”(x) = 2m² +36x² – 24mx

At x=0 (and hence at y=0):
g(0) = 0
g’(0) = 0
g”(0) = 2m²

Hence g”(0) is positive for all m≠0. Hence, from whichever direction we approach except from x-axis, (0,0) is a minima.

For m=0, the test fails. So, we handle it separately:
When m=0, i.e. f(x,0) = 3x⁴
We know that (0,0) is an absolute minima for this function.
Hence, (0,0) is a local minima for f(x,y) from this method.
---------------------------------------------------------------------------------
Now, we prove that (0,0) is surrounded by some negative points which contradicts the definition of local minima:
METHOD 3:
It’s simple, put y = 2x² in the function f(x,y):
So, f(x,2x²) = -x⁴.

On the x-y plane, y = 2x² is a parabola. Hence, all the values of the function f(x,y) on this parabola are negative. That means if we approach (0,0) while running on this parabola, we will always encounter negative values except at (0,0) where it is 0, hence on y = 2x², (0,0) is a maxima (absolute, infact).

Another important fact is that function at (0,0) is surrounded by some negative values, which contradicts the definition of local minima for a function in this case.
---------------------------------------------------------------------------------
METHOD 4:
I thought that going numerically and graphically will somewhat solve my problem. Here are some of my efforts:

The graph of f(x,y) (x from -0.002 to 0.002 and y from -0.000002 to 0.000002) amplified by 10¹² looks like this:

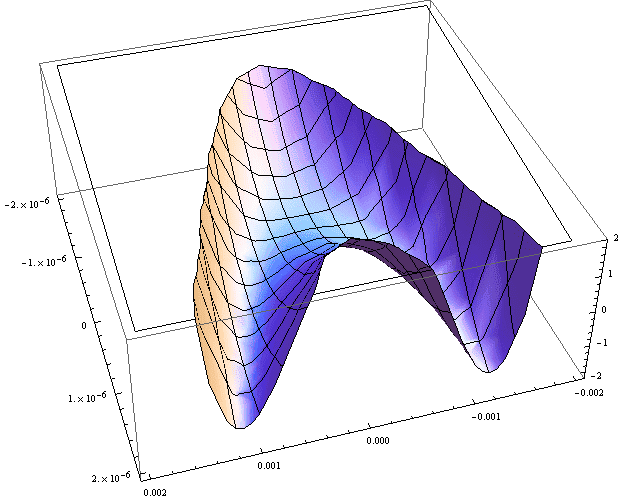
The graph was drawn using Mathematica 7.0 and the following command was used:
Plot3D[10¹² (y²+3x⁴-4y x²),{x,0.002,-0.002},{y,2*10^-6,-2*10^-6},PlotRange->{-2,2}]

The value of 10¹²f(±0.001,0.000002) = -1, calculated using mathematica.

 

[Billy Bob]

shanu_bhaiya, that is fantastic analysis!

By Method 2, you can correctly conclude that if you take a cross section of the surface where it intersects the vertical plane y=mx (z arbitrary), then you obtain a curve with local min at (0,0). However, you are not allowed to conclude that the surface itself has a local min there. (Your graph in Method 4 clearly shows there is a saddle there.)

So what's happening? To see it, graph the cross sectional curve y=3x^4-4mx^3+m^2 x^2, using m=1 to see a typical case. A good window is [-0.5,1.5] x [-0.2,0.1]. You'll see a local min at (0,0), a local max at approximately (0.21,0.01), and an absolute min at approximately (0.79,-0.18). The actual extrema are at x=0, x=(3-sqrt(3))/6, and x=(3+sqrt(3))/6.

The min at (0.79,-0.18) represents where your leg would rest if you were sitting in the saddle shown in Method 4, with your legs ahead of you (instead of hanging down directly by your side as they would with a hyperbolic paraboloid).

With the case of arbitrary m>0, the graph has the same general shape as the m=1 case, with the extrema at x=0, x=(3-sqrt(3))m/6 (approx x=0.2113m), and x=(3+sqrt(3))m/6 (approx x=0.7887m). Pay special attention to the fact that as m approaches 0, the "leg minimum" at x=0.7887m also approaches zero. The curve still has a local min at the origin, and yet with m approaching 0, you see that there are negative values of the surface z=f(x,y) (at the "leg minimum") arbitrarily close to the origin.

These "leg minimums" are consistent with what you found in Method 3, but here you looked only in the "leg rests."

The short answer is that since you yourself proved that z=f(x,y) takes on positive and negative values in any disk, in the domain, centered at the origin, then f has neither a local max nor a local min at (0,0).

But the longer analysis you provided (together with correction of your conclusions in Methods 2 and 3) is much more interesting, to me, than the short answer.

 

[shanu_bhaiya]

Thanks a lot for reply, I wasn’t even expecting one this time.
Hence this statement is wrong:
“For a function f(x,y), (x₀, y₀) is a local minima if it is a local minima of all those curves which are obtained by intersecting (y- y₀) = m(x- x₀) with f(x,y).”

As you said:

By Method 2, you can correctly conclude that if you take a cross section of the surface where it intersects the vertical plane y=mx (z arbitrary), then you obtain a curve with local min at (0,0). However, you are not allowed to conclude that the surface itself has a local min there. (Your graph in Method 4 clearly shows there is a saddle there.)

I cannot conclude that (0,0) is a local minima from method 2, that means the statement above must be wrong and correct statement will be:
“For a function f(x,y), (x₀, y₀) is a local minima if it is a local minima of all possible curves passing by (x₀, y₀).”
Is it correct?

Thanks a lot for giving the satisfactory solution. Although I have understood the story, I wanted to argue more. One last doubt is that book says "Prove that (0,0) is a local minima", I doubt if it means that (0,0) is really a local minima, but book may be wrong as well. Problem is officially solved, but I’m still waiting for a great statement which will give a deeper insight into the problem.