Nanocrystalline Ni-Mo alloys of various sizes

[HappyFlower]

Homework Statement

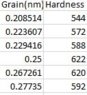
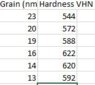
Nanocrystalline Ni-Mo alloys of various grain sizes (d) were prepared by electrodeposition. They showed the following hardness values.

Homework Equations

Ho=Hi + k/d^1/2

The Attempt at a Solution

1. Plot a hardness vs d^-1/2

Graph

3. Use best fit analysis and calculate the values for hall petch constants (Ho) and k for both sections of the graph.
I used a best fit line on the graph but a bit confused how this would help me. I don't know where to start at all. To find the hall-petch constants.

 

[Phylosopher]

You did not get a reply for more than 12 hours. I will give this a try. I know literally nothing about material science, after taking a look on wiki: grain boundary strengthening page, I don't think I understand the question properly!

If I would approach this problem like any other, I would say that the y-intercept in the graph is $H_{o}$, while the slope is the strengthening coefficient $k$.

Is this really your question? for someone taking material science this sounds like a very weird question. If this is not the what you are asking about, can you elaborate more and focus more on the exact issue rather than vaguely stating it? This will make it easier for people with no experience in materiel physics to help you.

 

[HappyFlower]

You did not get a reply for more than 12 hours. I will give this a try. I know literally nothing about material science, after taking a look on wiki: grain boundary strengthening page, I don't think I understand the question properly!

If I would approach this problem like any other, I would say that the y-intercept in the graph is $H_{o}$, while the slope is the strengthening coefficient $k$.

Is this really your question? for someone taking material science this sounds like a very weird question. If this is not the what you are asking about, can you elaborate more and focus more on the exact issue rather than vaguely stating it? This will make it easier for people with no experience in materiel physics to help you.

I think my professor wanted it to be a simple question and i am just over analyzing it. -,- I think you are right.

 

[mfb]

Side remark: I wouldn't trust that linear fit.