Need Help (teacher did not cover this)

[BunDa4Th]

Two packing crates of masses m1 = 10.0 kg and m2 = 3.50 kg are connected by a light string that passes over a frictionless pulley as in Figure P4.26. The 3.50 kg crate lies on a smooth incline of angle 44.0°. Find the acceleration of the 3.50 kg crate.
m/s2 (up the incline)

Find the tension in the string.
N

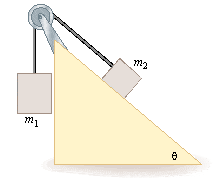
Okay so far I figure out that W1 = m1g = 98N and W2 = m2g = 34.3N and i think i did not even need to find that...

I need help on this because there are more problems like this and i can't seem to figure none of them out.

 

[arildno]

Set up a free body diagram. What forces act upon each block?
1. What does it mean that the block is SMOOTH?

2. What approximation can you do knowing that the string is LIGHT, and what does this entail, coupled with the knowledge that the pulley is FRICTIONLESS?

 

[BunDa4Th]

Well, I gave this another try and i am still at a lost but found out that acceleration for both block should be the same. (thats if i did my reading correctly)

any help or pointers would really help out since I tried the next problem since i thought it would help figure this out but i was wrong.

 

[arildno]

Ok, I'll bear out with you:
1. That the incline is SMOOTH means that it is FRICTIONLESS, that is on m2, the only forces acting upon it is gravity and tension. Likewise for m1.

2. That the string is LIGHT means that we may disregard its mass, and thus say the rope is massless. From Newton's 2-law of motion then, it follows that the sum of forces acting upon the string at all points must be zero, otherwise the rope would get infinite acceleration. Since the pulley is frictionless, only normal force and tension act upon the rope segment in contact with the pulley.

From this, it follows that the tension in the rope is CONSTANT throughout the rope.

3. As you've found out by yourself, because the string is inextensible, it follows that the magnitude of the blocks' accelerations must be the same.


That's all you need to solve the problem!

 

[civil_dude]

You need to come up with two equations for T. One for each block, and then set them equal to each other. Pay special attention to the 'direction' of acceleration when you do, i.e. assume a direction you think the blocks will move.