Need Help with Assignment? Let Me Check My Work for You!

[giant016]

I tried to post this before, but then when I hit post I was forced to see 5 other posts and it doesn't look like my post got put up, but I apologize if it did and I can't find it. Anyways, here we go again:

This assignment it kind of important, especially as the class is coming to an end. If I could get any of these problems checked I would greatly appreciate it. As you can see I am having some trouble on #3.

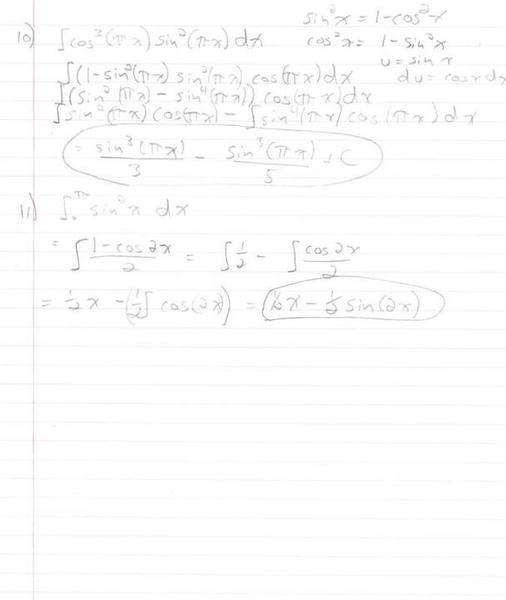
Thanks.

 

[Gib Z]

3) Just let ln(x) = u, then du= (1/x) dx and the integral is just \int u^2 du

7) is correct but set out extremely poorly. (x= infinity - x=1)??

8) You have the correct reasoning on the second line, the first line is the working for a different question, \lim_{a\to 0} \int^2_a x^{-3} dx

10) I can see that's incorrect because when you differentiate your result, you get factors of pi that you didn't account for. Check it.

 

[Dick]

And in 2) between the third and fourth lines a cos^2(2*phi) magically changes into a cos^2(phi). There should be a 4*phi term in the answer.