Need Help With Geometry Problem (Circles)

[Izzhov]

In the diagram below:

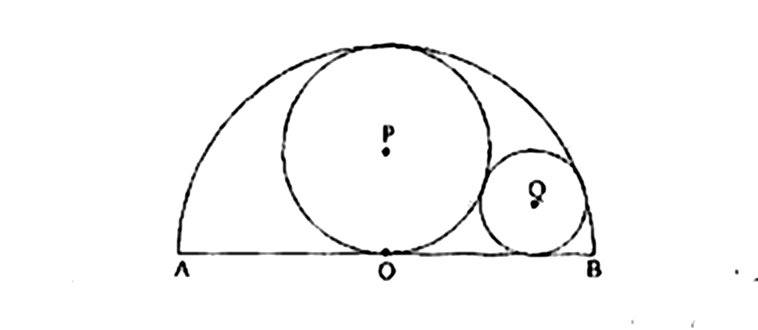
AB is the diameter of the semicircle with center O. Circles P and Q are tangent to each other and to the semicircle. If OB=4, find the radius of circle Q.

I haven't been able to make any headway at all with this problem. I tried to find a system of equations with the radius of circle Q equal to x and some other length equal to y, but all I found was that the length of the common external tangent of circles P and Q is $$2 \sqrt{2x}$$, where x is the radius of circle Q, and I'm not sure how that's useful. Please help.

 

[CarlB]

Let the origin be (0,0) in a cartesian coordinate system. The point P is then (0,2). Let the point Q be at position (x,y).

To define the position of a circle needs three equations. (There are 3 degrees of freedom, the position (x,y) of the center, and the radius.)

The radius of Q is y, this is one restriction.

The circle Q and P are tangent. This means that the distance from P to Q is equal to the sum of their radii.

The third restriction on the circle centered at Q is that it be tangent to the circle centered at O. This will be a quadratic equation in x and y.

 

[Izzhov]

Let the origin be (0,0) in a cartesian coordinate system. The point P is then (0,2). Let the point Q be at position (x,y).

To define the position of a circle needs three equations. (There are 3 degrees of freedom, the position (x,y) of the center, and the radius.)

The radius of Q is y, this is one restriction.

The circle Q and P are tangent. This means that the distance from P to Q is equal to the sum of their radii.

The third restriction on the circle centered at Q is that it be tangent to the circle centered at O. This will be a quadratic equation in x and y.

I'd already figured out the first two restrictions, and I understood that the third restriction would have to do with circle Q being tangent to the semicircle, but I have no idea how to derive an equation from that.

EDIT: Never mind. I figured it out. Thank you.