cuongbui1702
- 31
- 0
Example 23.2 in University Physics of Young and Freedman, i have a confusion with Negative work, positive work
In question b, Why the external force does a negative work (as i know, when you put three charges from infinity to the point of need identified, we will always do a force has the same way with objects)
Example 23.2:

My picture:
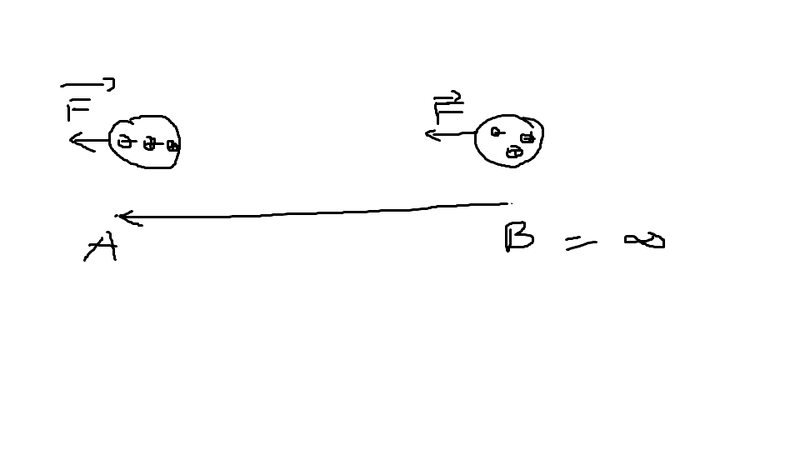
In question b, Why the external force does a negative work (as i know, when you put three charges from infinity to the point of need identified, we will always do a force has the same way with objects)
Example 23.2:
My picture: