Net displacement of a particle given its equation of motion

[javii]

Homework Statement

Hello PF,

I need some help with the assignment given:
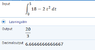
v=18-2t^2 m/s, where t is in second. When t= 0 the position of the particle is s_0 = - 3 m.
For the first 5 seconds.
Determine the total distance ( i got it to 65,33 ft) and the net displacement Δs, and the value of s at the end of the interval.

The Attempt at a Solution

I guess I have to use the formula:
s(t)=s_0 + ∫_0 ^t v(t) dt

s(t)=3+∫_0^3 18-2t^2 dt

 

[cnh1995]

s(t)=s_0 + ∫_0 ^t v(t) dt

That is the correct equation.
S₀= -3m.

 

[gneill]

... and t_f = 5 seconds.

 

[mfb]

Be careful with signs and units and integral borders. Apart from that, the total distance is fine, and the formula for s(t) will help with the net displacement Δs and s at the end.

 

[javii]

That is the correct equation.
S₀= -3m.

But when I integrate it, I do not get the correct answer.

 

[cnh1995]

But when I integrate it, I do not get the correct answer.

Why are you multiplying the integral by -3?
Also, the upper limit of the integral is not 3.

... and t_f = 5 seconds.

 

[javii]

Why are you multiplying the integral by -3?
Also, the upper limit of the integral is not 3.

May bad. So this should be correct?

 

[mfb]

That number is relevant. Which part did you answer with it?