Broem
- 9
- 0
Homework Statement
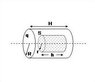
a cylindrical solid of charge q, radius R, and length H. The Gaussian surface S is a cylindrical shell of radius r and length h, with r < R. Determine the net electric flux given that q = -48Q, R = 4L, H = 3L, r = 2L, and h = 2L (type the integer value, along with the sign, without typing units Q/e0):
Homework Equations
Inet = Qenclosed / ε = δ A / ε
Vsphere = ∏r^2 h
The Attempt at a Solution
I've tried using my V in substitute for the A so:
-48Q*(∏2^2 * 2) / ε
But I am unable to find the correct solution. I'm really lost when it comes to this in theory. Also, the results in form Q/ε...I understand sort of. Do I use ε as 8.85E-12 or does it remain as just the known variable?
Please let me know how I can approach this and also how to ask this question better :)