Network analyzer on a single wire

[Thomas Rigby]

TL;DR Summary

I did this experiment and I don't understand the results

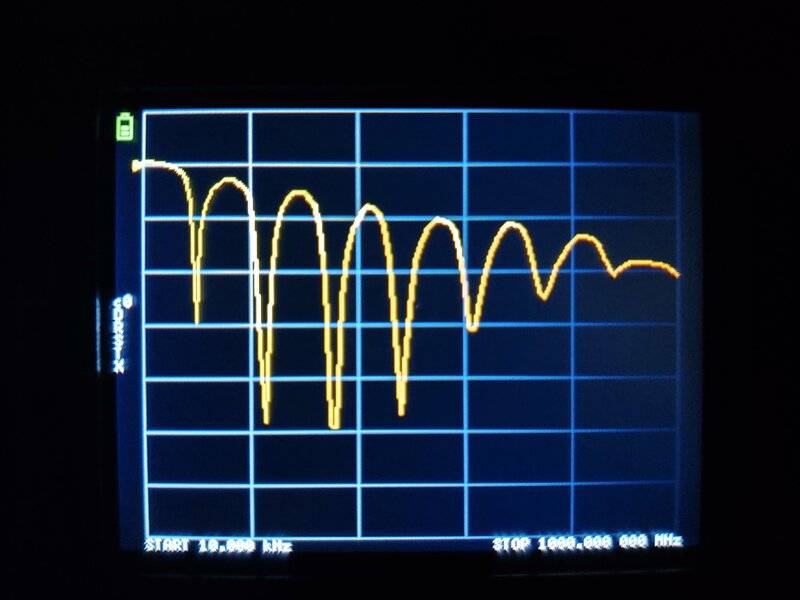
I have a NanoVNA spectrum analyzer. I took a 1 meter 12 AWG solid copper wire and soldered one end of that to the center conductor of the SMA connector and did a sweep from 10 kHz to 1 Ghz looking at reflection. I have attached a photograph of the result.

My hope is that someone can tell me what I am looking at. I have very little intuition in this regard, and will be learning from any responses
and requests for further details.

 

[berkeman]

Network Analyzer or Spectrum Analyzer? What are you measuring? Can you post a diagram of your test setup?

 

[Baluncore]

My hope is that someone can tell me what I am looking at.

The high value near zero tells me you are looking at an open-circuited transmission line, or an end-fed dipole antenna element.

When the reflection from the open end reinforces the drive there will be a high value.
When the reflection is out of phase with the drive there will be a dip.

You have an end-fed dipole antenna, 1 metre long. It will look most like an open circuit at λ = 2 metres. Then F = 300 / 2 = 150 MHz. That is why there is a hump at 150 MHz.

It will look like a short circuit when λ = 3 metres because the reflections will be out of phase.
300 / 3 = 100 MHz. Note the first dip is at 100 MHz.

 

[Baluncore]

You are doing Time Domain Reflectometry, but in the frequency domain. The reflected energy is attenuated for higher frequencies because it radiates from the wire antenna, so cannot be reflected. That also explains why the nulls are not as deep for higher frequencies.

I matched the position of the nulls to a transmission line simulation having a transit time of 3.6 ns, which gave a wire length of 3.6e-9 ns * 299792458 m/s = 1.079 m. Maybe;
1. You cut the wire 79 mm too long, or;
2. The wire had PVC insulation, giving a velocity factor of 1/1.079 = 92.7%, or;
3. You failed to calibrate the instrument with the short and open references provided, or;
4. I modeled it wrong.

 

[Thomas Rigby]

Thanks! This is very helpful.

 

[tech99]

As the wire becomes electrically long, the input impedance progressively cycles towards the characteristic impedance. Also not sure about the treatment of the ground side of the experiment.

 

[sophiecentaur]

You are doing Time Domain Reflectometry, but in the frequency domain.

Can you really describe the response of a circuit to a (swept) sinusoidal input as any form of Time Domain analysis? I think you may manage to confuse the poor OP. What the analyser is doing is 'Reflectometry by implication', surely.

 

[Baluncore]

Can you really describe the response of a circuit to a (swept) sinusoidal input as any form of Time Domain analysis?

Yes.
A frequency sweep is just a long, slow chirp. In the given example, phase information was available, but was not displayed. An FFT can be used to transform between the time and frequency domains, or to deconvolute the swept frequency chirp response into a TDR plot.

"Ground" is the poorly defined surrounding environment, the instrument, and the operator. Since the system is both a transmission line and a radiating wire antenna, the line losses are significant.

 

[tech99]

Regarding the swept frequency method, may I mention for interest that in 1924, by frequency modulating a Medium Wave broadcast transmitter and studying reflected signals, Edward Appleton created the first FM radar, and found evidence for the existence and height of an ionosphere, previously predicted by Kennelly in the USA and Heaviside in the UK. Of course, he did not have a computer. This work was at that time of great importance for communications, before the age of satellites, and Appleton received a Nobel for his work.

 

[sophiecentaur]

An FFT can be used to transform between the time and frequency domains, or to deconvolute the swept frequency chirp response into a TDR plot.

I wouldn't disagree with that but is it not accepted that the Fourier transform transforms between the time and frequency domains? A signal is a signal however you choose to describe it.

A standing wave measurement of a transmission line is very easy to make but interpreting the plot in terms of distances and discontinuities is a lot harder. Only explicit time domain analysis with pulses can give distance information conveniently.

Radar only became convenient when actual pulses with adequate peak powers were available for range information. Multipath distortion of a narrow band signal made early radio detection of targets very inconvenient.

 

[tech99]

Incidentally, a standing wave measurement does not necessarily give the information needed to find distance - it needs to be a plot of voltage or impedance. If we had a line with only one mismatch, the VSWR plot would be a straight line, giving no distance information.

 

[Baluncore]

Only explicit time domain analysis with pulses can give distance information conveniently.

The old style ionospheric sounders swept linearly from 2 to 30 MHz at about 1 MHz per second. I continuously multiply the reflected signal by the carrier, to get a difference frequency determined by the return delay time and the sweep rate. The carrier is rejected as a DC component.

For the 28 seconds of the sweep, I record the product as an audio signal in time. Then I take the FFT of that long record, to get an audio frequency power spectrum. That audio spectrum is a plot of the height of discontinuities in the atmospheric impedance above. There is no pulse required.

The use of the FFT gives a huge transform gain, that lifts very small impedance changes out of the noise, while reducing interference pulses by spreading them into the noise floor. The arguments for the use of swept TDR are the same as those for spread spectrum communications.

 

[sophiecentaur]

The arguments for the use of swept TDR are the same as those for spread spectrum communications.

We are clearly on different pages here. I'm not sure what a "swept TDR" is. Do you mean that the pulses are not regular?

In my, albeit a bit dated experience, I buy a TDR and it has a port which outputs a string of very fast pulses (a few ps with repetition period equal to at least twice the total cable length) the device then examines the reflected signal, in the time domain. Reflections are caused by impedance changes along the line and are represented (just like a Radar PPI) by the time trace on the screen. A gentle slope up or down on the trace represents series or shunt line resistances.
There are other ways to analyse a line, involving a swept frequency input signal. In my book, that is a frequency domain measurement. Which one is more suitable depends on the distances involved and what technology is available. TDR measurements of short feeders have not been available until relatively recently when suitably fast diodes became available. You can now 'see' the wiggles on a trace which corresponds to a dodgy (a few mm) connector assembly.

 

[Baluncore]

I'm not sure what a "swept TDR" is. Do you mean that the pulses are not regular?

I mean a TDR plot, obtained or computed from the swept sinewave of a network analyser. The technique is also called FDR.

We are clearly on different pages here.

We both understand the difference between the time and frequency domains.
You are classifying techniques by the test signal at the line electrical interface.
I am classifying techniques by the graphical interface to the human.

The TDR instruments used on long telephone trunk lines used a half-sine pulse, not the traditional, or textbook, steep edged square wave.

 

[sophiecentaur]

I mean a TDR plot, obtained or computed from the swept sinewave of a network analyser. The technique is also called FDR.


We both understand the difference between the time and frequency domains.
You are classifying techniques by the test signal at the line electrical interface.
I am classifying techniques by the graphical interface to the human.

The TDR instruments used on long telephone trunk lines used a half-sine pulse, not the traditional, or textbook, steep edged square wave.

Well that's OK then! No handbags at dawn needed.
The half sin shaped pulse would probably be more suitable for long lines with high loss which would produce reflected signals more like those from a Radar system. (An interesting practical detail)

 

[tech99]

If I may mention that the pulse was a sine squared pulse and was used for testing of video lines rather than telephony. Video is very sensitive to group delay distortion - easily seen with the pulse - but telephony is insensitive to it, so just ampitude testing will suffice. I seem to recall that the sine squared pulse contains frequencies up to 1/2T, where T is the half amplitude duration. For testing lower frequencies, a long rectangular pulse with sine squared edges was used.

 

[Baluncore]

If I may mention that the pulse was a sine squared pulse and was used for testing of video lines rather than telephony.

I was referring to the testing of telephony trunks, being long coaxial FDM bearers. https://en.wikipedia.org/wiki/Trunking

I thought the half-sine-like pulse was an approximation to sinc = sin(x)/x; the Fourier transform of which is rectangular, much like the pass-band of a trunk line and it's amplifiers. When ranging to faults over band-limited circuits, the pulse shape needed to remain symmetrical, to make the estimate of the reflection time more accurate. The width of the sinc pulse generated was selected to suit the bandwidth of the line or circuit under investigation.

It all gets a bit confused when I look closely at the details. I doubt a sin²(x) pulse could be used without an offset of phase and amplitude. Sin²(x) has an energy peak at twice the fundamental, then no further harmonics. Only when one cycle is isolated do other harmonics appear, and they are not spread evenly over the limited band.