Network Theory Problem do help

[lazyaditya]

1. Homework Statement
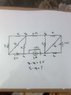
Va - Vb = 6 Volts
Calculate Vc - Vd = ?
The circuit diagram is shown below :-

All resistances are equal to "R" as shown in fig. except for 1 ohm and 2 ohm resisters.
Two voltage sources 10V and 5V are given and a current source in parallel to 1 ohm resistor.

Homework Equations

3. The Attempt at a Solution :
I thought of using KCl and nodal analysis method but the equations became quite complex.
Though i thought that the current flowing through 2 ohm resistor will be equal to current flowing in branch connecting Vc and Vd that will be 3 ampere using KCL.
Thus using kcl at node "M" current through 1 ohm resistor will be 5 ampere and thus voltage drop equals "5 volts = Vd - Vc". Therefore Vc - Vd equals -5 volts.

Am i doing it right and is there any other method to solve this question ?

 

[gneill]

Your reasoning and results are both correct. Well done.

 

[lazyaditya]

Thanks. But is there any other method to solve this problem ?

 

[gneill]

Thanks. But is there any other method to solve this problem ?

Well, even if you simplified the left and right portions of the network and wrote KVL and KCL equations, it would probably boil down (mathematically) to the same thing -- things would cancel here and there to leave you to draw the same conclusions.