Can the Newton's third law be violated in wires at right angles?

[hikaru1221]

So here is the problem:
2 thin straight wires carrying steady currents are placed perpendicular as shown in the attached file. The magnetic field at all points of the red wire due to the blue one is downward through the screen, and thus, the net force F exerting on the red wire due to the blue wire is upward and parallel to the blue wire. Similarly, the force F' that the blue wire experiences due to the red one is parallel to the red wire. So F and F' don't equal, which violates the Newton's 3rd law!
Was I wrong at some point here?
Thank you.

 

[atyy]

Are the wires infinitely long?

 

[hikaru1221]

^ No. Or you may consider them as parts of 2 infinitely long wires.

 

[hikaru1221]

Anyone, please? Is it too easy?

 

[jtbell]

Newton's third law does not apply in general to electromagnetic forces.

However, in classical mechanics, the third law is equivalent to conservation of the total momentum of a system. In electrodynamics, the total momentum of a system is still conserved, provided that you take into account the momentum carried by the electromagnetic field.

Conservation of momentum is more general than Newton's third law.

 

[hikaru1221]

Newton's third law does not apply in general to electromagnetic forces.

However, in classical mechanics, the third law is equivalent to conservation of the total momentum of a system. In electrodynamics, the total momentum of a system is still conserved, provided that you take into account the momentum carried by the electromagnetic field.

Conservation of momentum is more general than Newton's third law.

Thank you.
For electrostatic field and gravitation, the law might be still valid I guess (e.g. the force between 2 charges show such symmetry). Is it a coincidence, or is there an explanation for that? Is there any other case, i.e fields carrying momentum, where the law is violated?

 

[Dale]

It is not a coincidence, in a purely electrostatic field the field does not carry any momentum, so all of the momentum is carried by matter and Newton's 3rd law results.

 

[hikaru1221]

It is not a coincidence, in a purely electrostatic field the field does not carry any momentum, so all of the momentum is carried by matter and Newton's 3rd law results.

Oh but wikipedia says it does carry momentum.
http://en.wikipedia.org/wiki/Momentum#Momentum_in_electromagnetism

 

[Dadface]

So here is the problem:
2 thin straight wires carrying steady currents are placed perpendicular as shown in the attached file. The magnetic field at all points of the red wire due to the blue one is downward through the screen, and thus, the net force F exerting on the red wire due to the blue wire is upward and parallel to the blue wire. Similarly, the force F' that the blue wire experiences due to the red one is parallel to the red wire. So F and F' don't equal, which violates the Newton's 3rd law!
Was I wrong at some point here?
Thank you.

I don't think you've considered the geometry of the whole of each circuit .Remember that there is not a red and blue wire alone,there are connecting wires as well and the field at any point is due to the whole circuit and not just part of it.Newton's law is not necessarily violated here.

 

[hikaru1221]

I don't think you've considered the geometry of the whole of each circuit .Remember that there is not a red and blue wire alone,there are connecting wires as well and the field at any point is due to the whole circuit and not just part of it.Newton's law is not necessarily violated here.

But you know, in the universe, there are many planets besides Earth and Sun, but the 3rd law can still be applied for the interaction between Earth and Sun only. The 3rd law doesn't require the system to be isolated.

 

[Dadface]

But you know, in the universe, there are many planets besides Earth and Sun, but the 3rd law can still be applied for the interaction between Earth and Sun only. The 3rd law doesn't require the system to be isolated.

But the force on each wire is due to the whole of each circuit.The effects of the connecting wires etc cannot be considered as negligible in this problem as it was presented.Consider a very long current carrying wire.In the centre of the wire we can assume,to a good first approximation,that the field pattern is circular and concentric to the wire.This assumption becomes less valid as we move towards each end of the wire because now the circuit becomes non linear.

 

[hikaru1221]

But the force on each wire is due to the whole of each circuit.The effects of the connecting wires etc cannot be considered as negligible in this problem as it was presented.Consider a very long current carrying wire.In the centre of the wire we can assume,to a good first approximation,that the field pattern is circular and concentric to the wire.This assumption becomes less valid as we move towards each end of the wire because now the circuit becomes non linear.

Force on each wire = force of the other wire + force of the rest of the two circuits.
But the 3rd law states that: force on 1st wire due to 2nd wire = force on 2nd wire due to 1st one. Just like the example about Earth and Sun: Earth experiences forces due to many planets, but force on Earth due to Sun = force on Sun due to Earth. The 3rd law doesn't care whether the forces due to other planets are negligible or not.

 

[Dadface]

Force on each wire = force of the other wire + force of the rest of the two circuits.
But the 3rd law states that: force on 1st wire due to 2nd wire = force on 2nd wire due to 1st one. Just like the example about Earth and Sun: Earth experiences forces due to many planets, but force on Earth due to Sun = force on Sun due to Earth. The 3rd law doesn't care whether the forces due to other planets are negligible or not.

I am assuming you considered the field shape and field direction around each wire and then applied the left hand rule or similar.If so fine but the field at the edge where the wires meet is not circular in the way described.In order to work out the force at each point on each wire you have to take into account the field at that point due to the other circuit.

 

[hikaru1221]

I am assuming you considered the field shape and field direction around each wire and then applied the left hand rule or similar.If so fine but the field at the edge where the wires meet is not circular in the way described.In order to work out the force at each point on each wire you have to take into account the field at that point due to the other circuit.

I still don't get your point. The wires don't have to intersect each other. Even if they are, the force on the edge is too small comparing to the total force on the other points on the wires, so it wouldn't matter much.
And again, what's the point of considering the rest of the circuit, when the 3rd law only focuses on the interaction between the 2 wires?

 

[ehild]

Would you say that Newton's 3rd law is violated in the problem in the figure with two boxes interacting through a string? Box 1 acts with a vertical force on box 2 while box 2 acts with a horizontal force on box 1.

ehild

 

[hikaru1221]

No. The forces are due to the string. The boxes don't interact with each other directly. I guess you mean the magnetic field is like the string, right? (so thank you for giving me a great analogy)
So is it like the forces are the result of the interaction between each wire/current and the magnetic field created by the other wire, or between each wire and the magnetic field formed by both, or between both magnetic fields formed by both wires?

 

[ehild]

Correct, I meant so that the electromagnetic field is something like a string between two objects. Well, it is very difficult... Using fields is an approximation already. And the magnetic field interacts with the electrons moving in the wire instead of the wire itself. And an electron does not interact with its own field. I think it would better to speak about interaction of the electrons moving in the wires, taking into account that this interaction is not instantaneous.
Anyway, Newton's 3rd law is one of the postulates of Classical Mechanics, in inertial frames of reference. Electromagnetism is beyond Classical Mechanics. You certainly will study Relativity Theory, and then you'll get a more accurate description of such phenomena. I know two little for that.

ehild

 

[Dadface]

I still don't get your point. The wires don't have to intersect each other. Even if they are, the force on the edge is too small comparing to the total force on the other points on the wires, so it wouldn't matter much.
And again, what's the point of considering the rest of the circuit, when the 3rd law only focuses on the interaction between the 2 wires?

Hello again hikaru.Your circuit is not real,its imaginary.You could make it real by extending the length of each wire and taking each end of each wire to the poles of a battery.This is equivelent to adding connecting wires and now your wires are not straight along their whole length.When you consider the field set up by each wire you should consider the whole wire and not the straight bits only.In your thought experiment you ignored the contribution to the field from the non straight(connecting wire)bits even though these connecting wires carry the same current and are probably longer than the straight bits.There is not a "rest of the circuit" which is irrelevant as you imply, the connecting wires are an integral part of the whole circuit and the field contribution due to them increases as you approach the edges of the straight sections.

 

[hikaru1221]

Correct, I meant so that the electromagnetic field is something like a string between two objects. Well, it is very difficult... Using fields is an approximation already. And the magnetic field interacts with the electrons moving in the wire instead of the wire itself. And an electron does not interact with its own field. I think it would better to speak about interaction of the electrons moving in the wires, taking into account that this interaction is not instantaneous.
Anyway, Newton's 3rd law is one of the postulates of Classical Mechanics, in inertial frames of reference. Electromagnetism is beyond Classical Mechanics. You certainly will study Relativity Theory, and then you'll get a more accurate description of such phenomena. I know two little for that.

ehild

Thank you very much, ehild. So:
1 - Why is using fields an approximation?
2 - Why can't an electron interact with its own field? The field is like another entity and "touches" the electron, so why not? If I consider a charged sphere moving freely, it will emit electromagnetic wave and thus, lose energy gradually, which means there must be some force (though infinitesimal) decelerating it, is that correct?
3 - Since you mentioned electron, I guess you mean each magnetic field "acts on its own", which means each field due to each moving electron can be discriminated somehow. Or things are like there is only one magnetic field (summing up all the magnetic fields) besides currents?
Any reply would be appreciated very much.

Hello again hikaru.Your circuit is not real,its imaginary.You could make it real by extending the length of each wire and taking each end of each wire to the poles of a battery.This is equivelent to adding connecting wires and now your wires are not straight along their whole length.When you consider the field set up by each wire you should consider the whole wire and not the straight bits only.In your thought experiment you ignored the contribution to the field from the non straight(connecting wire)bits even though these connecting wires carry the same current and are probably longer than the straight bits.There is not a "rest of the circuit" which is irrelevant as you imply, the connecting wires are an integral part of the whole circuit and the field contribution due to them increases as you approach the edges of the straight sections.

Thank you for your patience.
Oh yes, there certainly are things besides the straight wires. But why do we have to consider the whole circuit, when we only care about the interaction between the 2 wires?
So how would you find the force that one wire (not the whole circuit) exerts on the other?

 

[Dadface]

hikaru,you can use Biot and Savarts law to calculate the value of B and in many geometries,including the central portion of a long straight wire,you can ,to a good approximation,ignore the contribution from the connecting wires.In your circuit you are considering the field close to the junction where the straight wire and connecting wire meet and this is at a place where the contribution due to the connecting wire(which can be considered as an extension of the straight wire) is not negligible.We do "care about the interaction between the two wires" but the two wires are not made of the straight sections only.

 

[hikaru1221]

hikaru,you can use Biot and Savarts law to calculate the value of B and in many geometries,including the central portion of a long straight wire,you can ,to a good approximation,ignore the contribution from the connecting wires.In your circuit you are considering the field close to the junction where the straight wire and connecting wire meet and this is at a place where the contribution due to the connecting wire(which can be considered as an extension of the straight wire) is not negligible.We do "care about the interaction between the two wires" but the two wires are not made of the straight sections only.

I'm sorry, I haven't got your point yet.
The two wires here are parts of 2 circuits, and those two wires are particularly made straight. Then I use the Biot-Savarts law to calculate B due to one wire at the other wire so that I can calculate the force that one wire exerts on the other, which is my main purpose and also where the problem comes from. So I don't understand why considering B value due to the rest, because that doesn't mean the effect of the rest is negligible, it's just that all I care is the force between the wires.

 

[Dadface]

I'm sorry, I haven't got your point yet.
The two wires here are parts of 2 circuits, and those two wires are particularly made straight. Then I use the Biot-Savarts law to calculate B due to one wire at the other wire so that I can calculate the force that one wire exerts on the other, which is my main purpose and also where the problem comes from. So I don't understand why considering B value due to the rest, because that doesn't mean the effect of the rest is negligible, it's just that all I care is the force between the wires.

The magnitude and orientation of the force at any location on each wire depends,amongst other things,on the magnitude and orientation of B at that location due to the opposite wire.The value of B depends on the whole circuit and not just part of it.You have deliberately made two sections of wire straight but these sections make up less than fifty percent of the total circuit.How can you justify considering only a certain part of a circuit whilst ignoring the bulk of that circuit?As I have stated before there are many geometries where the effects of the rest of the circuit can be ignored but your circuit is not one of these for reasons I have already pointed out.
I think the main problem here is that yours is a thought experiment and you have possibly not considered what is needed to make it into a real experiment.Try sketching out your circuit diagram again but with each straight section of wire connected to its power supply.

 

[hikaru1221]

The magnitude and orientation of the force at any location on each wire depends,amongst other things,on the magnitude and orientation of B at that location due to the opposite wire.The value of B depends on the whole circuit and not just part of it.You have deliberately made two sections of wire straight but these sections make up less than fifty percent of the total circuit.How can you justify considering only a certain part of a circuit whilst ignoring the bulk of that circuit?As I have stated before there are many geometries where the effects of the rest of the circuit can be ignored but your circuit is not one of these for reasons I have already pointed out.
I think the main problem here is that yours is a thought experiment and you have possibly not considered what is needed to make it into a real experiment.Try sketching out your circuit diagram again but with each straight section of wire connected to its power supply.

The B value at one point is due to the whole circuit, I agree with that point. However, in order to find the force between the 2 wires only (there is force by the rest of the circuit which is NOT negligible), I calculate B due to one wire only and then deduce the force from that. So is that an incorrect way to calculate the force that one wire exerts on the other? If so, then how would you calculate it?

 

[Dadface]

The B value at one point is due to the whole circuit, I agree with that point. However, in order to find the force between the 2 wires only (there is force by the rest of the circuit which is NOT negligible), I calculate B due to one wire only and then deduce the force from that. So is that an incorrect way to calculate the force that one wire exerts on the other? If so, then how would you calculate it?

I'm not sure what you're asking here but I'll have a guess.It seems that you want to calculate the force between the two straight sections of wire only and ignore the effects of the rest of the circuit.To a good approximation you can do this if the geometry is such that the rest of the circuit is very remote from the two sections of straight wire you are considering.One example of this would be if the wires are parallel and very long.In fact this arrangement is used to define the ampere(the definition states that the wires are infinitely long)
It's all well and good ignoring the rest of the circuit in such arrangements but look again at the arrangement you presented and see if you can draw it in full with the rest of the circuit being very remote from the region you are considering.

 

[hikaru1221]

I'm not sure what you're asking here but I'll have a guess.It seems that you want to calculate the force between the two straight sections of wire only and ignore the effects of the rest of the circuit.To a good approximation you can do this if the geometry is such that the rest of the circuit is very remote from the two sections of straight wire you are considering.One example of this would be if the wires are parallel and very long.In fact this arrangement is used to define the ampere(the definition states that the wires are infinitely long)
It's all well and good ignoring the rest of the circuit in such arrangements but look again at the arrangement you presented and see if you can draw it in full with the rest of the circuit being very remote from the region you are considering.

Yes, that's what I'm trying to do, but I'm not ignoring the effect of the rest (I mean, it's not negligible); it's just that I only consider the force F between the 2 straight wires (or straight sections as you call). So the problem is the method: I calculate B due to one section, and then, use that B to calculate F. If the method is correct, then the 3rd law is violated.

Okay, here is a circuit which satisfies the conditions you make (see picture). The power supplies are far away from the straight wires. I make the connecting wires particularly in that shape so that the B field due to them is canceled. Is it a circuit that you want?

 

[Dadface]

Yes, that's what I'm trying to do, but I'm not ignoring the effect of the rest (I mean, it's not negligible); it's just that I only consider the force F between the 2 straight wires (or straight sections as you call). So the problem is the method: I calculate B due to one section, and then, use that B to calculate F. If the method is correct, then the 3rd law is violated.

Okay, here is a circuit which satisfies the conditions you make (see picture). The power supplies are far away from the straight wires. I make the connecting wires particularly in that shape so that the B field due to them is canceled. Is it a circuit that you want?

hikaru,can you see it from your own diagram now?To have your two wires arranged as shown in your original diagram requires that some of the connecting wires are not remote from your straight(coloured in red) wires.look at the bottom horizontal connecting wire of the top circuit and the left vertical wire of the bottom circuit.Consider these two wires as a set and consider the two red wires as a set and now compare the two sets.There is a certain symmetry between the two sets and the two circuits and because of the geometry of the system you can see that the set of connecting wires can be just as dominant as the set of red wires.The resultant field at a point due to each circuit is due to the whole circuit and not just part of it and the 3rd law refers to the resultant force on each circuit not just the component of the force on one part of that circuit.Of course the connecting wires can be of any length and shape but you will always have some of them in close proximity to your red wires.

 

[hikaru1221]

hikaru,can you see it from your own diagram now?To have your two wires arranged as shown in your original diagram requires that some of the connecting wires are not remote from your straight(coloured in red) wires.look at the bottom horizontal connecting wire of the top circuit and the left vertical wire of the bottom circuit.Consider these two wires as a set and consider the two red wires as a set and now compare the two sets.There is a certain symmetry between the two sets and the two circuits and because of the geometry of the system you can see that the set of connecting wires can be just as dominant as the set of red wires.The resultant field at a point due to each circuit is due to the whole circuit and not just part of it and the 3rd law refers to the resultant force on each circuit not just the component of the force on one part of that circuit.Of course the connecting wires can be of any length and shape but you will always have some of them in close proximity to your red wires.

In the original diagram, I DID NOT draw any complete circuit, I only drew 2 straight wires in order to illustrate my point. Anyway, did you look at my new one? The connecting wires are made in special shape and the wires connected directly to the power supplies are far away from the red ones, so that I can totally ignore their contribution to B value at points near the red straight wires.

The resultant field at a point due to each circuit is due to the whole circuit and not just part of it and the 3rd law refers to the resultant force on each circuit not just the component of the force on one part of that circuit.

This gave me a pause.

I agree that "The resultant field at a point due to each circuit is due to the whole circuit and not just part of it", and so "the resultant force on something is due to the whole circuit".

But the Newton's 3rd law NEVER refers to any particular force. Instead, it says if one of the straight wires exerts force F on the other one, then the other one exerts force F'=-F on the 1st one. The law doesn't care if it is net force or not, if there is something else besides the straight wires or not.

That's why I didn't consider the effect of the rest of the circuit in the calculation. All I need is the forces between the straight wires.

 

[Dadface]

In the original diagram, I DID NOT draw any complete circuit, I only drew 2 straight wires in order to illustrate my point. Anyway, did you look at my new one? The connecting wires are made in special shape and the wires connected directly to the power supplies are far away from the red ones, so that I can totally ignore their contribution to B value at points near the red straight wires.

Look again at what you drew originally.The lines of the wires,when extended,do not cross through each other but meet at a point and at an angle of 90 degrees.You had current passing through the wires but no circuits or power supplies to provide those currents.Let's overlook these omissions for the moment.Something crucial to the point you were making is the shape of the field and you assumed that at the important location at the ends of the wire the field is circular.Its circular around the mid section of the wire but when you proceed to the edges and beyond the field shape and strength changes. I don't know how it changes with your imaginary circuit but nor do you.In fact there are no fields at all in the imaginary circuit and there are no forces.
Now let's look at the real circuits and look at the field shapes at the important locations at the edges(and beyond)What you have now is a complete direction change where you straight wires meet your connecting wires.So now what are the shapes of the fields that meet the opposite wires at the points under consideration?

This gave me a pause.

I agree that "The resultant field at a point due to each circuit is due to the whole circuit and not just part of it", and so "the resultant force on something is due to the whole circuit".

But the Newton's 3rd law NEVER refers to any particular force. Instead, it says if one of the straight wires exerts force F on the other one, then the other one exerts force F'=-F on the 1st one. The law doesn't care if it is net force or not, if there is something else besides the straight wires or not.

That's why I didn't consider the effect of the rest of the circuit in the calculation. All I need is the forces between the straight wires.

But the forces between the straight wires are there as a consequence of the whole circuits.

 

[hikaru1221]

Look again at what you drew originally.The lines of the wires,when extended,do not cross through each other but meet at a point and at an angle of 90 degrees.You had current passing through the wires but no circuits or power supplies to provide those currents.

I didn't draw the full circuit or the power supply doesn't mean they're not there. Sorry for making this confusion. In the original picture, I only focused on the straight currents and so, I assumed that they were in the circuits though I didn't drew completely.

Something crucial to the point you were making is the shape of the field and you assumed that at the important location at the ends of the wire the field is circular.Its circular around the mid section of the wire but when you proceed to the edges and beyond the field shape and strength changes. I don't know how it changes with your imaginary circuit but nor do you.In fact there are no fields at all in the imaginary circuit and there are no forces.
Now let's look at the real circuits and look at the field shapes at the important locations at the edges(and beyond)What you have now is a complete direction change where you straight wires meet your connecting wires.So now what are the shapes of the fields that meet the opposite wires at the points under consideration?

Why is the field around the end of the wire not circular? By applying Biot-Savarts law, we can see that the B field due to the straight sections at those points is circular (and in the new picture, the rest doesn't contribute at all to the B field). And why is there no force?
Could you draw some diagram to illustrate your point?

But the forces between the straight wires are there as a consequence of the whole circuits.

In a set of 3 things A, B and C:
_ Force on A = force of B on A + force of C on A
_ Force on B = force of A on B + force of C on B
_ Newton's law: (force of B on A) = - (force of A on B)
The forces due to the whole things are (force on A) and (force on B), but the forces between A and B are (force of B on A) and (force of A on B).

Even if it is as you define, then in my new picture, the rest of the 2 circuits don't contribute to the B field, and so, they don't exert any force on the straight wires. Thus, in the new diagram, the forces due to each wire and the forces due to the whole circuits are the same.

 

[Dadface]

I didn't draw the full circuit or the power supply doesn't mean they're not there. Sorry for making this confusion. In the original picture, I only focused on the straight currents and so, I assumed that they were in the circuits though I didn't drew completely.



Why is the field around the end of the wire not circular? By applying Biot-Savarts law, we can see that the B field due to the straight sections at those points is circular (and in the new picture, the rest doesn't contribute at all to the B field). And why is there no force?
Could you draw some diagram to illustrate your point?

When I said there is no force I was referring to the imaginary circuit not a real one.In your analysis you are assuming that the field around a long straight wire is circular and in a plane at 90 degrees to the wire.This can be a good first approximation assumption in a real circuit which can be constructed with any connecting wires etc at such a great enough distance that their effects can be considered as negligible.Your analysis requires that you go to the edge of one of the straight wires,the shape and orientation of the field at this place being central to the analysis you are making.The problem is that going to an edge necessitates that you come into close proximity with a connecting wire,you can no longer ignore the rest of the circuit.

In a set of 3 things A, B and C:
_ Force on A = force of B on A + force of C on A
_ Force on B = force of A on B + force of C on B
_ Newton's law: (force of B on A) = - (force of A on B)
The forces due to the whole things are (force on A) and (force on B), but the forces between A and B are (force of B on A) and (force of A on B).
I'm not sure what you are saying here but in the example we are discussing here the force on each section of a circuit is due to the B field at that section due to all conducting parts of the opposite circuit.
Even if it is as you define, then in my new picture, the rest of the 2 circuits don't contribute to the B field, and so, they don't exert any force on the straight wires. Thus, in the new diagram, the forces due to each wire and the forces due to the whole circuits are the same.

Hikaru when Biot and Savarts law is used to find the value of B around a straight wire the integration is carried out from one end of the wire to the other.In this analysis we are located exactly at one end of a wire where there is a sudden change of direction and any integration needs to be carried out over the whole circuit.The resultant field and its orientation change at the edge.

 

[hikaru1221]

Your analysis requires that you go to the edge of one of the straight wires,the shape and orientation of the field at this place being central to the analysis you are making.

I don't get it. I consider the whole straight wire, not only a small part at the edge. So even if at the edge, the B field is a bit different (not circular), but at most points on the straight wire, it is still circular, so this makes little difference.

Hikaru when Biot and Savarts law is used to find the value of B around a straight wire the integration is carried out from one end of the wire to the other.In this analysis we are located exactly at one end of a wire where there is a sudden change of direction and any integration needs to be carried out over the whole circuit.

I don't get it neither. Do you mean that when calculating B, we MUST ALWAYS compute the integral over the whole complete circuit? And what do you mean by "we are located exactly at one end of a wire"?

First, look at my second picture. The B due to connecting wires is zero because of their shape, and the power supplies are located very far from the considered points. So even if I do the integration over the whole circuit, the result will turn out to be the same as when I only consider the straight section.

Second, I calculate B in order to calculate force, this is my main purpose. In the example about 2 parallel long straight wires, to calculate force between them, we calculate B due to ONE wire and then use the formula F=BIL to calculate force on the other wire. In other words, calculating B due to everything in my problem leads to nowhere, because I cannot calculate the force between the straight sections from that result!

How would you calculate the force that one straight section exerts on the other straight section? I think I will comprehend your point if you answer this question. Thank you very much.

 

[Dadface]

Hello hikaru,
in your opening post you marked in the force direction on the "straight wires".Before we take this any further can I ask you to look at the circuit you drew(post 25) and mark in the force direction on all four sides of each circuit.Having done this do you still think the third law is violated?

 

[hikaru1221]

Hello hikaru,
in your opening post you marked in the force direction on the "straight wires".Before we take this any further can I ask you to look at the circuit you drew(post 25) and mark in the force direction on all four sides of each circuit.Having done this do you still think the third law is violated?

Consider the left circuit.
The upper side consists of many parallel sections, or many couples of parallel sections which carries currents in opposite direction. Because in each couple, the sections are close to each other and so the B fields at the sections are approximately the same. Thus, the total force on the side is zero. And the same thing for the opposite side.
For the connecting wire connected to the power supply, I'm stumped, because the B field due to the power supply is unpredictable. I can't conclude anything here.

Okay, back to a point that I want to make clear. Again, I cite some lines I wrote before:
"In a set of 3 things A, B and C:
_ Force on A = force of B on A + force of C on A
_ Force on B = force of A on B + force of C on B
_ Newton's law: (force of B on A) = - (force of A on B)
The forces due to the whole things are (force on A) and (force on B), but the forces between A and B are (force of B on A) and (force of A on B)."
I don't consider the forces that the 2 circuits exert on each other. I only care about the forces that the straight sections exert on each other.

 

[Dadface]

Hello,I will take your second point first.
I can understand your reasoning if,for example, A,B and C were masses and we were calculating gravitational attractions.In this case there would be a force between A and B even if C weren't there.I think your reasoning works for other types of interaction as well but I can't yet see how it works for the system we are discussing.Suppose A and B are defined to be the straight sections of wire on the left hand and right hand circuits respectively and let C be the rest of the right hand circuit.We can describe the force on A or on a section of A but we cannot describe how much of this is due to B only.Unlike the gravitational or other cases we cannot ignore C because without C, B would not have a current through it and would not set up a magnetic field.The force in A is due to the field from the whole of the opposite circuit.
As for your first point just apply the left hand rule to all four sides of each circuit just as you did in your opening post where you applied it to one side only.The fields set up by each circuit will bear some similarities to the field shape set up by a circular coil the most important feature being that the field lines cut the plane containing the circuits at 90 degrees.
hikaru,I hope this is getting you thinking as much as it is me

 

[hikaru1221]

Hello,I will take your second point first.
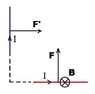
I can understand your reasoning if,for example, A,B and C were masses and we were calculating gravitational attractions.In this case there would be a force between A and B even if C weren't there.I think your reasoning works for other types of interaction as well but I can't yet see how it works for the system we are discussing.Suppose A and B are defined to be the straight sections of wire on the left hand and right hand circuits respectively and let C be the rest of the right hand circuit.We can describe the force on A or on a section of A but we cannot describe how much of this is due to B only.Unlike the gravitational or other cases we cannot ignore C because without C, B would not have a current through it and would not set up a magnetic field.The force in A is due to the field from the whole of the opposite circuit.

As for your first point just apply the left hand rule to all four sides of each circuit just as you did in your opening post where you applied it to one side only.The fields set up by each circuit will bear some similarities to the field shape set up by a circular coil the most important feature being that the field lines cut the plane containing the circuits at 90 degrees.
hikaru,I hope this is getting you thinking as much as it is me

What you mean here is we are unable to find a force on A due to B only; only the total force on A can be found, right? But how about the rest of the circuit containing A? I think we should include it in C.

Okay, before digging deeper, I want to ask you some more:

1. You say we cannot find the force that A exerts on B only. Is this due to:
- the limitation of our ability to perceive (?!)
- or because A and B cannot exist without C,
- or the force doesn't exist?

No comment for the 1st one. For the 3rd one, if the force due to each part doesn't exist, then the force due to everything won't exist. And for the 2nd one, it is obvious that no C, no A and B, no force; but the situation here is that A, B and C exist at the same time, so A and C should exert forces on B together. If we can find the total force A and C exert on B, that means we can find the force A exerts on B, because A is current and C is also current, they share the same nature (the magnetic field is due to current, not circuit, because even if there is one moving electron, magnetic field exists; so I think only the characteristics of current matters here. Besides A can no way perceive that it is permitted to exert force on B because there is C; A should act independently from C).

The only reasonable explanation I found is that the force on B is due to neither A nor C; it is due to the magnetic field - another "thing" besides A, B and C, which leads me to the questions in post #19.

2. This idea is quite silly, but just to expand the problem. Imagine that I can make a machine which can shoot "FAST electron beam", and the machine has a structure which prevents the EM field generated by the machine to the outside. Now back to the 1st picture. Instead of 2 wires, I place 2 machines shooting beams which are perpendicular to each other and don't intersect. No circuit, but there are currents. The force's nature changes, but we can find the forces between the beams.

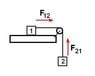
3. I don't get your point about the forces in the 2nd picture in post #25. The circuits in this picture are special, as I have already pointed out in some posts. The most important thing in this picture is that at the points near the red straight sections, total B field = B field due to the sections only.

Arguing with me is quite tiring, huh?

 

[Dadface]

hikaru,I think all your questions will be most easily answered if you carry out the little exercise I described in post 32.You did it for your straight wires in the opening post so you should be able to manage it for the rest of the circuit.Consider your left hand circuit and the resultant field this sets up.The field lines make closed loops and the most relevant feature of the pattern is that field lines cut the plane of both circuits by 90 degrees.If you can't see it use any suitable text to look at the field set up by a narrow circular coil.For a square,rectangular or other shaped circuit the field pattern will be different but the 90 degree angle still applies.Now look at this field passing through your right hand circuit and work out the direction of the force on each side in turn.You will see that if the force direction on the top wire is upwards(as in your op) then the force direction on the bottom wire is downwards,the force direction on the left vertical wire is to the left and the force direction on the right vertical wire is to the right(sorry to be long winded but I don't know how to send diagrams).The force on each side weakens with distance from the closest edge and from this you will see that the resultant force on the right hand circuit will be pointing up at an angle to the horizontal and towards the left hand circuit.By extending your analysis you will see that the resultant force on the left hand circuit points towards the right hand circuit.
Initially I found the analysis here to be quite difficult but when I got a mental picture of the resultant field pattern due to each circuit it became much easier.

If course this doesn't prove that the forces are exactly opposite in direction and nor does it prove that the forces are equal in magnitude.

 

[hikaru1221]

Have you looked at my circuit at post #25?

 

[ehild]

I think you will find this interesting.

http://www.df.lth.se/~snorkelf/Longitudinal/Slutdok.html

ehild

 

[Dadface]

Have you looked at my circuit at post #25?

I have looked .It was the circuits you drew in post 25 that I was referring to in post 36.Try out the exercise and hopefully you will see what I am getting at.

 

[hikaru1221]

@ehild: Thank you very much. I haven't finished reading yet but it's surprisingly interesting.
@Dadface:
This is what I see in my circuit:
_ Consider the left circuit. In the upper side, each pair of wires has 2 currents going in opposite directions, so the element dB due to the pair is zero and the external force on the pair is zero. The same for the opposite side.
_ The left side which connects the power supply is very far, so we can consider this isolated from the external magnetic field. This side experiences no external force and don't contribute to the B field at the space near the red side.
_ This leaves alone the two red sections, and so, the external force that each circuit experiences is the same as the force that each straight wire experiences and perpendicular to the straight wire.
Did I miss your point?

 

[Dadface]

This is what I see in my circuit:
_ Consider the left circuit. In the upper side, each pair of wires has 2 currents going in opposite directions, so the element dB due to the pair is zero and the external force on the pair is zero. The same for the opposite side.
_ The left side which connects the power supply is very far, so we can consider this isolated from the external magnetic field. This side experiences no external force and don't contribute to the B field at the space near the red side.
_ This leaves alone the two red sections, and so, the external force that each circuit experiences is the same as the force that each straight wire experiences and perpendicular to the straight wire.
Did I miss your point?

I think I'm missing your point.When you refer to the upper side and each pair of wires what pair are you referring to? I am guessing that you are referring to the two vertical sections of wire and if so it is the same current going in opposite direction.The field doesn't cancel out and somewhat resembles the field you would get around a very short solenoid.Its true that the more distant parts of the circuit have a smaller effect but the "connecting wires"at the near edges of the circuits are just as close as the "red wires".

 

[hikaru1221]

Short solenoid? You mean it's like "flattened solenoid"?
The field doesn't cancel out, it simply nearly equals to zero. When it's too small, why counts it?

 

[Dadface]

I think you will find this interesting.

http://www.df.lth.se/~snorkelf/Longitudinal/Slutdok.html

ehild

Thank you ehild.I scanned it and my first impression is that there is some interesting stuff but I would need to invest a lot of time to understand it properly.

 

[Dadface]

Short solenoid? You mean it's like "flattened solenoid"?
The field doesn't cancel out, it simply nearly equals to zero. When it's too small, why counts it?

I counted it because you counted it.Your circuits can be considered as flattened solenoids of square or rectangular cross section and consisting of one turn only.B is small but it's not zero.

 

[hikaru1221]

Oh so you mean the circuit is a short flattened retangular solenoid with one turn. I thought you were saying about the upper side's wire in post #41.
Yes, I agree with that, we can consider it so. However as I pointed out, the B field around the red section is mostly due to the red section only. And about the pair, yes, I referred to the 2 vertical sections carrying opposite currents (or the same current going in opposite directions). And the B field due to the pair is nearly zero. That's what I meant in post #42.

 

[Dadface]

Try the exercise hikaru.

 

[hikaru1221]

I think this is your exercise, right?

hikaru,I think all your questions will be most easily answered if you carry out the little exercise I described in post 32.You did it for your straight wires in the opening post so you should be able to manage it for the rest of the circuit.Consider your left hand circuit and the resultant field this sets up.The field lines make closed loops and the most relevant feature of the pattern is that field lines cut the plane of both circuits by 90 degrees.If you can't see it use any suitable text to look at the field set up by a narrow circular coil.For a square,rectangular or other shaped circuit the field pattern will be different but the 90 degree angle still applies.Now look at this field passing through your right hand circuit and work out the direction of the force on each side in turn.You will see that if the force direction on the top wire is upwards(as in your op) then the force direction on the bottom wire is downwards,the force direction on the left vertical wire is to the left and the force direction on the right vertical wire is to the right(sorry to be long winded but I don't know how to send diagrams).The force on each side weakens with distance from the closest edge and from this you will see that the resultant force on the right hand circuit will be pointing up at an angle to the horizontal and towards the left hand circuit.By extending your analysis you will see that the resultant force on the left hand circuit points towards the right hand circuit.
Initially I found the analysis here to be quite difficult but when I got a mental picture of the resultant field pattern due to each circuit it became much easier.

If course this doesn't prove that the forces are exactly opposite in direction and nor does it prove that the forces are equal in magnitude.

I agree that at all points in the plane of the circuits, the B field is perpendicular to the plane, there is no doubt about this.

Consider the right circuit:
_ The force on the red wire (the top one) is upward (1)
_ The force on the bottom wire is downward (2)
_ The left side: If it's straight, the force is obviously to the left. But it's more complicated when in fact, it's not. However I can predict that the force is nearly to the left, i.e. its horizontal component >> its vertical component. And the same for the right side. (3)

However:
_ For (1), it's obvious.
_ For (2), since it's too far from the rest of the circuit, plus that the B field due to the left and right sides is nearly zero as I explained, the force is nearly zero.
_ For (3), the force is nearly zero too as I explained.

 

[Dadface]

You can't see it so try this:
Take two long parallel pieces of straight wire each with connecting wires and a battery. Do you agree that the third law applies to this situation.Next take the middle section of each wire and bend it so that there is a corner with a 90 degree angle.Keep the wires in the same plane with the corners closest and facing.Do you agree that the third law applies to this situation the only difference being that the force per current element gets smaller as you proceed from the middle points to the edges.Now look at the circuits you drew but turn your diagram through 45 degrees.

 

[hikaru1221]

I still can't see your point. Your example is perfectly symmetrical. Mine is not.

 

[Dadface]

I still can't see your point. Your example is perfectly symmetrical. Mine is not.

So shift my example along so that it matches yours.It makes no difference and you can draw the circuits and how they are arranged in a whole variety of ways.It's the principle you should be looking at.