Newton's Law & Gravitational F: Finding the Accl'n for a sphere

AI Thread Summary
To find the initial acceleration of the third sphere in the equilateral triangle setup, apply Newton's law of universal gravitation, which states that the gravitational force between two masses is proportional to the product of their masses and inversely proportional to the square of the distance between them. Given the two spheres with a mass of 2.8 kg each and the distance of 1.20 m, calculate the gravitational force exerted on the third sphere by each of the two spheres. The net force acting on the third sphere can be determined by vector addition of these forces. Finally, use Newton's second law (F=ma) to find the acceleration of the third sphere by dividing the net force by its mass. The solution requires careful consideration of the forces and angles involved in the equilateral triangle configuration.
BootyBabe
Messages
1
Reaction score
0

Homework Statement


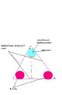
Three uniform spheres are located at the corners of an equilateral triangle. Each side of the triangle has a length of 1.20m. Two of the spheres have a mass of 2.8 kg, each.

The third sphere has an unknown mass, and is released from rest.

Considering only the gravitational forces that the spheres exert on each other, find magnitude of the initial acceleration of the third sphere.


Homework Equations






The Attempt at a Solution



I'm not sure how to attempt this question, where do I start> thanks!
 

Attachments

  • untitled.JPG
    untitled.JPG
    11.4 KB · Views: 462
Physics news on Phys.org
Start with Newton's law of universal gravity.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'Collision of a bullet on a rod-string system: query'

Thread 'Collision of a bullet on a rod-string system: query'

In this question, I have a question. I am NOT trying to solve it, but it is just a conceptual question. Consider the point on the rod, which connects the string and the rod. My question: just before and after the collision, is ANGULAR momentum CONSERVED about this point? Lets call the point which connects the string and rod as P. Why am I asking this? : it is clear from the scenario that the point of concern, which connects the string and the rod, moves in a circular path due to the string...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Newton's law of gravitation, find the mass and radius of the sphere
Replies
8
Views
2K
Gravitational Force on three spheres
Replies
17
Views
14K
Newton's first law, forces, charges
Replies
4
Views
2K
How to calculate the gravitational field outside of a sphere
Replies
8
Views
2K
Why do you integrate to find the gravitational field?
Replies
3
Views
1K
Question regarding Coulomb's Law
Replies
8
Views
1K
Masses in a Triangle - Gravitational Force
Replies
8
Views
5K
Determine the direction and acceleration of the bead
Replies
6
Views
4K
Sphere rolling with slipping on a movable platform
Replies
1
Views
2K
How to Rank Charge Density of Conductive Spheres?
2
Replies
61
Views
5K

Hot Threads

Recent Insights

Back
Top