Eitan Levy
- 259
- 11
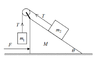
Homework Statement
No friction between m2 and M.
The static friction between M and the floor is μs and the dynamic is μd.
When F=0, what is the minimal static friction if M doesn't move?
Homework Equations
F=ma
Force caused by friction: μN=F
The Attempt at a Solution
What I thought is that m2 is affected by gravity, normal and tension and that M is affected by m2's normal, gravity, it's own normal and the friction.
I wrote the following equations:
N=m2gcosθ
Ncosθ+Mg=N' (N' is M's normal).
Nsinθ=μsN'
My answer:
μs=m2gsinθcosθ/(Mg+m2gcos2θ)
Their answer:
What am I missing here?