- #1
hypermorphism
- 506
- 1
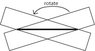
This one's just cute, but it's pretty easy (did it on a napkin at McDonald's when I was bored  ). We all know that given a line segment, we can easily construct a perpendicular bisector with a straight edge and a compass. The challenge is to construct a perpendicular bisector to a given line segment of unknown length using only a straight edge, in a finite amount of steps (and a pencil, of course). The straight edge is a rectangle, but cannot be used to measure the length of the line segment.
). We all know that given a line segment, we can easily construct a perpendicular bisector with a straight edge and a compass. The challenge is to construct a perpendicular bisector to a given line segment of unknown length using only a straight edge, in a finite amount of steps (and a pencil, of course). The straight edge is a rectangle, but cannot be used to measure the length of the line segment.