Nodal analysis voltage confusion

Click For Summary
SUMMARY

The discussion centers on the confusion regarding nodal analysis in electrical circuits, specifically the voltage across resistors R1 and R2. The voltage across R2 is defined as vT-0 = vT, while the voltage across R1 is expressed as vT-Vs1. Participants seek clarification on the nodes involved in these voltage measurements and the application points of the voltage source Vs1. The circuit diagram provided specifies the connections for Vs1, which is crucial for accurate analysis.

PREREQUISITES
  • Nodal analysis in electrical circuits
  • Understanding of voltage sources and their connections
  • Familiarity with resistor voltage drop calculations
  • Basic circuit diagram interpretation skills
NEXT STEPS
  • Review the principles of nodal analysis in electrical engineering
  • Study the application of voltage sources in circuit analysis
  • Learn how to calculate voltage drops across resistors in series and parallel configurations
  • Examine circuit diagrams to identify nodes and connections accurately
USEFUL FOR

Electrical engineering students, circuit designers, and anyone involved in analyzing and troubleshooting electrical circuits will benefit from this discussion.

princejan7
Messages
93
Reaction score
0
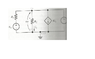
So the voltage across the R2 resistor is given as vT-0 = vT

But then the voltage across the R1 resistor is given as "vT-Vs1"
I'm not sure which two nodes the voltage across R2 involves. Is it the same as R1?

Also, I am not sure of the voltage source vs1. Across which two points does it apply?
 

Attachments

  • Untitled.png
    Untitled.png
    31.7 KB · Views: 434
Physics news on Phys.org
Can you identify the nodes in your circuit? The diagram specifies explicitly where Vs1 is connected...
 

Similar threads

Ohm's Law - Finding Source Voltage
  • · Replies 3 ·
Replies
3
Views
2K
Connecting a number of EMF sources in a circle to form a circuit
  • · Replies 9 ·
Replies
9
Views
1K
Nodal analysis with dependent voltage source
  • · Replies 4 ·
Replies
4
Views
2K
Understanding example in Wikipedia entry for open circuit voltage
  • · Replies 3 ·
Replies
3
Views
2K
RC Circuit with parallel resistor
  • · Replies 6 ·
Replies
6
Views
3K
Identical Batteries in Parallel do not Draw Same Current, Non-Ideal?
  • · Replies 7 ·
Replies
7
Views
1K
Simple Voltage-Divider: Design the voltage divider to provide 5V output
  • · Replies 23 ·
Replies
23
Views
6K
Finding Optimal Fixed Resistor for Potential Divider Circuit
  • · Replies 45 ·
2
Replies
45
Views
4K
Finding the Voltage across a Resistor using the Node Voltage Method
  • · Replies 2 ·
Replies
2
Views
3K
General DC Circuit: Voltage drop different from supply source
  • · Replies 29 ·
Replies
29
Views
3K