Simple Voltage-Divider: Design the voltage divider to provide 5V output

[sugz]

Homework Statement

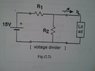
The attached figure shows a simple voltage-divier connecting a dc voltage source to a variable resistive load. Design the voltage divider to provide a voltage of about 5V (+/- 10%) across the variable load. The load-current demand varies in the range of 0 to 5mA, and the available dc-supply voltage is 15V.

Homework Equations

V=IR
equivalent resistance across parallel circuits: R1*R2/(R1+R2)
equivalent resistance across the series circuit: R1+R2

The Attempt at a Solution

I understand that the voltage across the Load is 5V, which would mean that the voltage across the R2 resistor is also 5V. This would mean that the voltage drop across R1 is 10V since KVL states the sum of voltages across a loop must be zero. I also know that the voltage divider rule states that the voltage across V(R2)=15*(R2/R1+R2).

I am not sure how to move forward from here. Please help

 

[gneill]

The voltage to the load is allowed to vary +/-10% as the load current varies between 0 and 5 mA. At the extremes of the current values, what load voltages would you associate with them? Can you write expressions for those two cases? (hint: you might consider using nodal analysis for the 5 mA case).

 

[sugz]

The voltage to the load is allowed to vary +/-10% as the load current varies between 0 and 5 mA. At the extremes of the current values, what load voltages would you associate with them? Can you write expressions for those two cases? (hint: you might consider using nodal analysis for the 5 mA case).

This would mean I would first assume 0 mA through the load and find what the voltage is across it. Wouldn't this make the voltage across the load be 0 since V=IRm where I is zero. Then 5 mA through the load and write an expression for what the voltage would be across the load? The question is asking to design the voltage divider to provide a voltage of about 5V (+/- 10%) across the variable load. What is this really asking me to find?

The equations I have is:

1) voltage across R2:
V2=15*R2/(R1+R2)

2) voltage across Load when IL is 0 mA

Vload=(IL)*Rload

3) voltage across Load when IL is 5 mA

Vload=5mA*Rload.

Not sure where to go from here.

 

[gneill]

This would mean I would first assume 0 mA through the load and find what the voltage is across it and then 5 mA through the load and write an expression for what the voltage would be across the load? The question is asking to design the voltage divider to provide a voltage of about 5V (+/- 10%) across the variable load. What is this really asking me to find?

It wants you to choose resistors for the voltage divider such that when the load current varies between 0 and 5 mA the load voltage stays in the range 5 V +/- 10% .

5 V +/- 10% tells you what the minimum and maximum voltages are. You should be able to make an educated deduction as to which of the two current extremes are associated with each of those voltages. Write expressions for the two scenarios incorporating those voltage&current pairs.

 

[sugz]

It wants you to choose resistors for the voltage divider such that when the load current varies between 0 and 5 mA the load voltage stays in the range 5 V +/- 10% .

5 V +/- 10% tells you what the minimum and maximum voltages are. You should be able to make an educated deduction as to which of the two current extremes are associated with each of those voltages. Write expressions for the two scenarios incorporating those voltage&current pairs.

Hi,
I created two scenarios, with one where voltage across the variable load is 5.5V and another case where voltage is 4.5V across the variable load. The voltage across R2 will then be 5.5V for the first case and 4.5V for the second case since they are in parallel. The voltage across R1 will then be 9.5V and 10.5V, respectively. I attempted to write expressions for the two scenarios but I am lost on the part on how to find the load current at the extreme of the voltages. Please help?

 

[gneill]

You're given two load currents. Can you associate them with the appropriate load voltages?

 

[sugz]

You're given two load currents. Can you associate them with the appropriate load voltages?

0mA for the 4.5V and 5mA for the 5.5V across the load?

 

[gneill]

0mA for the 4.5V and 5mA for the 5.5V across the load?

No, think about it a bit more. If the load current increases, what's that going to do to the voltage drop across R1? Will there be more or less voltage left for the load? Big shiny hint: Suppose the load tried to draw an extreme amount of current, say by making it a short circuit?

 

[sugz]

No, think about it a bit more. If the load current increases, what's that going to do to the voltage drop across R1? Will there be more or less voltage left for the load? Big shiny hint: Suppose the load tried to draw an extreme amount of current, say by making it a short circuit?

if the load current increases, the the voltage would then decrease across R1. If the variable load draws an extreme amount of current,then you would have almost 0 resistance through the variable load right since its now become short circuited. in addition, we are assuming the variable load resistance is kept constant? sorry if i made a nymistakes but i am really trying hard to understand this.

 

[gneill]

No you can assume that the load is changing resistance. That's why the current demand changes.

So at the extreme when the load heads to a short circuit condition the load current would be high and the load voltage would be low (like zero volts), right? Then R1 would be dropping all of the source voltage. That is, the drop across R1 increases as the load current increases. This makes sense because the more voltage that's dropped across R1, the less is available for the load. And in the extreme, all of it is dropped on R1 and the load current is maximized (R1 effectively being the only resistance in the circuit).

So using that principle you should be able to match up the given voltage and current pairs.

 

[sugz]

No you can assume that the load is changing resistance. That's why the current demand changes.

So at the extreme when the load heads to a short circuit condition the load current would be high and the load voltage would be low (like zero volts), right? Then R1 would be dropping all of the source voltage. That is, the drop across R1 increases as the load current increases. This makes sense because the more voltage that's dropped across R1, the less is available for the load. And in the extreme, all of it is dropped on R1 and the load current is maximized (R1 effectively being the only resistance in the circuit).

So using that principle you should be able to match up the given voltage and current pairs.

In the case where the load current is maximized, which is 5mA, the load voltage would be low (0V). As you mentioned, this will make the R1 the only element of the circuit, where the entire source voltage is dropped across R1. Therefore, voltage across V(R1)=I1*R1. Here we assume R1=1 kohms, which means the equation becomes 15=I1*1k, which gives I1 as 15mA, where I1 is the current through R1 resistor. Now, I know that R1=1kohms and current through it is 15mA. Another equation I have is I1=I2+I3, where I2 is the current through I2 and I3 is the current through the LOAD. Any idea how I move forward? I am going to assume I should analyze the second extreme where the current across the LOAD is zero, which would mean its an open circuit. Is this correct?

 

[gneill]

In the case where the load current is maximized, which is 5mA, the load voltage would be low (0V).

Noooooo. The lower allowed voltage is 4.5 V. The 0 V case was a hypothetical extreme to get the idea across of what happens to the load voltage as the load current increases.

As you mentioned, this will make the R1 the only element of the circuit, where the entire source voltage is dropped across R1. Therefore, voltage across V(R1)=I1*R1. Here we assume R1=1 kohms, which means the equation becomes 15=I1*1k, which gives I1 as 15mA, where I1 is the current through R1 resistor. Now, I know that R1=1kohms and current through it is 15mA. Another equation I have is I1=I2+I3, where I2 is the current through I2 and I3 is the current through the LOAD. Any idea how I move forward?

You have two cases. Each case has a voltage and current pair associated with it. You should now know which pair of voltage and current belongs to each case.

One of the cases has no load current (IL = 0). Write the expression for the voltage divider that produces the voltage associated with this case.

The other case has a load current of 5 mA. Write an expression for the voltage divider that produces the voltage associated with this case.

You should now have two equations in two unknowns (R1 and R2). Solve!

 

[sugz]

Noooooo. The lower allowed voltage is 4.5 V. The 0 V case was a hypothetical extreme to get the idea across of what happens to the load voltage as the load current increases.


You have two cases. Each case has a voltage and current pair associated with it. You should now know which pair of voltage and current belongs to each case.

One of the cases has no load current (IL = 0). Write the expression for the voltage divider that produces the voltage associated with this case.

The other case has a load current of 5 mA. Write an expression for the voltage divider that produces the voltage associated with this case.

You should now have two equations in two unknowns (R1 and R2). Solve!

Hi, thank you so much for your help! I understand I have taken long to understand the concept but its people like you who allow me to continue to try and finally understand the concept. The pairs will be 4.5V for 5mA and 5.5 for 0mA. I hope you are able confirm this for me.

 

[gneill]

Hi, thank you so much for your help! I understand I have taken long to understand the concept but its people like you who allow me to continue to try and finally understand the concept. The pairs will be 4.5V for 5mA and 5.5 for 0mA. I hope you are able confirm this for me.

Confirmed!

 

[sugz]

Hi, this is the calculation I performed for the two cases. However, I noticed that with two unknowns (R1 and R2), I end up with the two equations as shown in the attached document. I used the voltage divider rule to get these equations. Do j make an assumption for one of the resistors and the second one is dependent on tbr first one I assume? It seems as if this is the only way it can work out.

 

[gneill]

Hi, this is the calculation I performed for the two cases. However, I noticed that with two unknowns (R1 and R2), I end up with the two equations as shown in the attached document. I used the voltage divider rule to get these equations. Do j make an assumption for one of the resistors and the second one is dependent on tbr first one I assume? It seems as if this is the only way it can work out.

Your case 1 is good, only the figure shouldn't show 5 mA current for the load, since the case if for IL = 0 mA.

The second case is not so good. You've not included the 5 mA load current in your derivation. I suggest using nodal analysis to do so easily; the load current just becomes another term in the node equation.

You will end up with two equations in two unknowns. They can be solved for R1 and R2.

 

[sugz]

Yes, you are correct. I intended the voltage across the load in the first case to be 4.5 and not 5.5. I will redo this part again. For case 2 where IL is 0mA, I thought since the load current is 0mA, I would not included it in my derivation. Am I missing somwthing?

 

[gneill]

Yes, you are correct. I intended the voltage across the load in the first case to be 4.5 and not 5.5. I will redo this part again. For case 2 where IL is 0mA, I thought since the load current is 0mA, I would not included it in my derivation. Am I missing somwthing?

The figure headings say: "Case 1: I_L = 0 mA" and "Case 2: I_L = 5 mA". The accompanying circuit diagrams say the opposite. But in fact your work for Case 1 reflects the no current scenario: there's no load current in the equations, and it uses the 5.5 V maximum voltage as expected for a no-load case.

Unfortunately the Case 2 labelled work also shows no current, despite the header which says it should.

You need to include the 5 mA load current and 4.5 V output voltage in your equation for the loaded case.

 

[sugz]

Sorry about the confusion. I must have not been thinking straight as it was very late. I have re-done the steps again, which has been attached here. Case 2 (IL=5mA) seems good. All I need to do is solve for R1 or R2 in case 1 and substitute it into Case 2 equation to solve for the resistor value. However, I have a question related to Case 1. when IL =0, wouldn't we not have a voltage drop across it since V=IR? I am not sure how to calculate the Resistor of the LOAD when IL=0. I am going to try to answer this..Please correct me if I am wrong. When IL=0, the load part of the circuit becomes an open circuit, leaving only R1 and R2, where the voltage across R2 is 5.5V.

 

[gneill]

Don't use V/R form for the load current in the node equation. You aren't given a particular load resistor value (and it's obviously changing from case to case). Just use the current value itself, it's much simpler. The terms of a node equation represent branch currents.

When the load current is zero then yes, it's equivalent to an open circuit. This is the same as putting '0' for the load branch current in the node equation.

 

[sugz]

You are totally amazing! I believe I have figured it out. The values were R1=545.45 ohms and R2=315.9 ohms. Although this was actually simple, with your guidance, I have learned a lot of concepts which I would have not if someone had simply given the answer. I have attached my steps here for reference. Thanks again for your patience and help!

 

[gneill]

Looks good! Glad I could help. Keep practicing, and good luck with your studies!

 

[sugz]

Hi,

I have one last question related to case 1 where the load current is 0 mA. How is the voltage 4.5 when the load current is 0. Should it not be 0 as well since it has to be v=IR?

 

[gneill]

Hi,

I have one last question related to case 1 where the load current is 0 mA. How is the voltage 4.5 when the load current is 0. Should it not be 0 as well since it has to be v=IR?

When the load current is 0 mA then the output voltage 5.5 V. But that's not so important now.

When the load current is zero then the load resistance is equivalent to an infinite resistance. That is the same as it being removed entirely. No matter what voltage you put across it there will be zero current flow.