Non-uniform Hanging Bar: Finding the Center of Mass

[typeinnocent]

Homework Statement

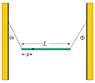
The bar is of nonuniform density so one end is heavier than the other. It has an overall length of 6.9 meters and is held in place by two very light wires. The left cord makes an angle with the wall of Θ = 39 degrees and the right cord makes an angle of Φ = 52 degrees.

Homework Equations

Net torque must equal zero, and the forces in the x and y direction must each equal zero.

The Attempt at a Solution

For net torque:
T2(cos52)(6.9-x)-T1(cos39)(x)-mg(3.45-x)=0 (with m being the mass of the bar)
For net force in the x direction:
T2(sin52) = T1(sin39)
For net force in the y direction:
T1(cos39)+T2(cos52) = mg

My pivot point was the center of mass, shown by the dot on the picture. Using these equations, I let T2 = T1(sin39/sin52). Then I substituted what mg equals into the net torque equation, and also substituted what T2 equals into the net torque equation. All of the T1's cancel out, and I'm able to solve for x. But the answer is incorrect. Any suggestions as to what I'm doing wrong?

 

[LowlyPion]

Welcome to PF.

I can't see your picture, but what is it you are trying to solve for?

X the center of mass?

If you are taking your sum of torques about the center of mass then don't you sum just the moments of the vertical components? The mg of the bar is presumably acting through the center of mass and has a 0 moment doesn't it? And the horizontal components are equal but likewise acting with 0 moment.

 

[typeinnocent]

Oops, sorry! I am solving for the distance x from the left side of the bar to its center of mass. Since the bar is of non-uniform density, the center of mass isn't at the center of the bar.
(hopefully the picture below will show. I'm still learning how the posting works.)
https://wug-s.physics.uiuc.edu/cgi/courses/shell/common/showme.pl?cc/DuPage/phys2111/summer/homework/Ch-12-Equilibrium/hanging-bar/hanging-bar.gif

 

[ideasrule]

"For net torque:
T2(cos52)(6.9-x)-T1(cos39)(x)-mg(3.45-x)=0 (with m being the mass of the bar)"

Net torque with respect to which point? The first two terms, T2cos(52)(6.9-x) and T1(cos 39)(x), both seem to suggest you're using the center of mass as the reference point. If that's the case, gravity exerts no torque because it can be seen as acting on the center of mass, so the moment arm is 0.

 

[typeinnocent]

Thank you both so much! You're both correct; the pivot point was the center of mass and I was including it in my calculations when I shouldn't have. Apparently even though I read that the pivot point was the center of mass, part of my internal being still wanted the center of mass at the center of the bar...

 

[turandorf]

So what part of T2(cos52)(6.9-x)-T1(cos39)(x)-mg(3.45-x)=0 or the other equations still work if you use the center of mass as a pivot point? I also am confused about the mass, as it is not given and you need it to find tension. If anyone could explain that would be great! :)

 

[ideasrule]

So what part of T2(cos52)(6.9-x)-T1(cos39)(x)-mg(3.45-x)=0 or the other equations still work if you use the center of mass as a pivot point? I also am confused about the mass, as it is not given and you need it to find tension. If anyone could explain that would be great! :)

Because gravity exerts no torque, the mg(3.45-x) term shouldn't be there; the equation should just be T2(cos52)(6.9-x)-T1(cos39)(x). The other equations deal with forces, with torques, and they remain valid.

 

[turandorf]

Ok that makes sense but I am confused by the system of equations. Usually one of the tensions is possible to find in a numeric form. But since we do not have the mass, how is that possible?(eg. T2=(T1sin(Θ))/sin(Φ) but how do you find T1?)

 

[typeinnocent]

The tensions actually don't need to be found. Once I had the correct torque equation, I substituted T1(sin39/sin52) in for T2, and the T1's cancel out completely, leaving you with only x to solve for.

 

[turandorf]

So did you end up with an equation that looked like
(sin(Θ)/sin(Φ))cos(Φ)(6.9-x)=cos(Θ)x
?

 

[typeinnocent]

Yes, that looks correct.

 

[turandorf]

ok thanks to all for the help! You all are grade-savers!