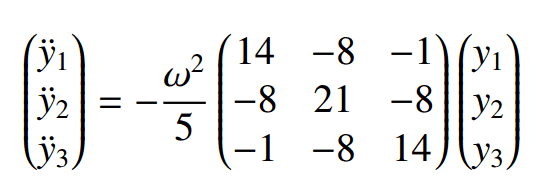SUMMARY
The discussion focuses on finding eigenfrequencies corresponding to the normal modes of a system described by the eigenvectors $$(1,0,-1), (1,1,1), (1,-2,1)$$. The participants express confusion regarding the method to calculate these eigenfrequencies, as the source material only provided the results without the underlying process. The need for a clear step-by-step approach to derive eigenfrequencies from given eigenvectors is emphasized.
PREREQUISITES
- Linear algebra concepts, specifically eigenvalues and eigenvectors
- Understanding of normal modes in mechanical systems
- Familiarity with matrix operations and characteristic equations
- Basic knowledge of differential equations related to oscillatory systems
NEXT STEPS
- Study the process of calculating eigenvalues from a matrix using the characteristic polynomial
- Learn how to derive eigenfrequencies from eigenvalues in mechanical systems
- Explore examples of normal mode analysis in coupled oscillators
- Investigate the application of these concepts in real-world physical systems
USEFUL FOR
Students in physics or engineering, researchers in mechanical systems, and anyone interested in the mathematical foundations of oscillatory motion and normal mode analysis.