Jhenrique
- 676
- 4
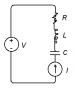
The equation for this physical model is:
http://upload.wikimedia.org/wikipedia/commons/f/fb/RLC_series_circuit_v1.svg

And for this is:
http://upload.wikimedia.org/wikipedia/commons/d/d0/RLC_parallel_circuit_v1.svg
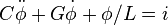
But and if now I add a source of current in those schemes, the ODE changes?
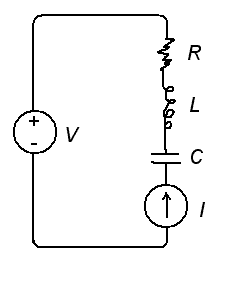
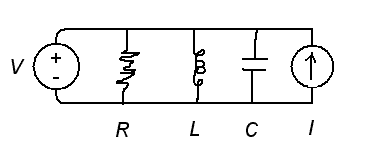
http://upload.wikimedia.org/wikipedia/commons/f/fb/RLC_series_circuit_v1.svg
And for this is:
http://upload.wikimedia.org/wikipedia/commons/d/d0/RLC_parallel_circuit_v1.svg
But and if now I add a source of current in those schemes, the ODE changes?