On deriving response function in simple low pass filter

[Emspak]

Homework Statement

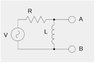
I have a problem where the circuit is as follows: (pic attached I hope) but if you can't see it it's just a power source (AC), resistor and inductor with 2 terminals across the inductor (from were you measure the voltage).

I want to derive the response function, and I am trying to see if I did something off. I am doing it in terms of frequency, rather than $\omega$.

Homework Equations

So I know that the resistance in an inductor is $Z_L = iL\omega$
Resistance from a resistor is just R

Response function $H ( \omega) = \frac{V_{out}}{V_{in}}$

The Attempt at a Solution

So I take the whole circuit and see these are in series. So the total resistance ($Z_{total} = R + iL\omega$.

That means the current in the circuit is $\frac{V_{in}}{R + iL\omega }$

and the $V_{out} = \frac{V_{in}R}{R + iL\omega }$ because we are measuring the voltage across the inductor.

Substitute omega with f/2pi and we get
$$V_{out} = \frac{V_{in}R}{R + iL\frac{f}{2\pi} } \rightarrow \frac{V_{out}}{V_{in}} = \frac{2\pi R}{2\pi R + iLf} = H ( f)$$

Is there anything wrong with this? I ask because I'm doing a lab and even accounting for experimental error my Bode plot diverges a lot from the measured numbers. The shape of the curves is all good; just the one I plotted above seems moved to the right and up a bit from the values I got. Same shape exactly, tho. Not a big deal I guess, but I wanted first and foremost to make sure I did this right.

 

[zoki85]

That means the current in the circuit is $\frac{V_{in}}{R + iL\omega }$

and the $V_{out} = \frac{V_{in}R}{R + iL\omega }$ because we are measuring the voltage across the inductor.

But this is not the voltage across inductor what you wrote

 

[Emspak]

Let me guess: it should have been $V_{out} = \frac{V_{in} \omega L}{R+ \omega L}$, right?

 

[zoki85]

What happened to i ?

 

[Emspak]

Typo. $V_{out} = \frac{V_{in} i \omega L}{R+i \omega L}$