Whitebread
- 21
- 0
I don't quite understand how the modified goodman equation can be applied to a multiaxial stress state. The explanation given in my stress analysis class has been quite confusing and verbose so I've come here to see if I can't get a better understanding.
First I'll lay out what I think to be true:
Utilizing the Von-Mises failure criterion in place of the uni-axial stresses in the goodman equation should be able to account for a multiaxial stress state AND fatigue. Here's how I think it should work
Uni-axial stress amplitude is replaced with von-mises stress amplitude (same equation, different stresses)
The fatigue limit at whatever number of cycles the designer is concerned with is replaced with the Von-Mises stress at that stress amplitude. Or: (Uni-Axial Fatigue limit at X cycles)*(1/3)=fully reversed stress amplitude (or SIGMAar in the good man equation).
Mean stress is replaced with mean von-mises stress (same equation, different stresses)
Ultimate stress is replaced with (sqrt(2)/3)*SIGMA(u) or the von mises stress at failure.
Equations:
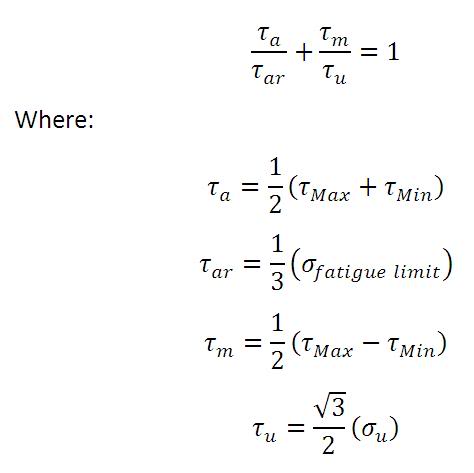
That last equation should be sqrt(2)/3. Made a mistake when writing the equations. Thanks.
Is this correct?
First I'll lay out what I think to be true:
Utilizing the Von-Mises failure criterion in place of the uni-axial stresses in the goodman equation should be able to account for a multiaxial stress state AND fatigue. Here's how I think it should work
Uni-axial stress amplitude is replaced with von-mises stress amplitude (same equation, different stresses)
The fatigue limit at whatever number of cycles the designer is concerned with is replaced with the Von-Mises stress at that stress amplitude. Or: (Uni-Axial Fatigue limit at X cycles)*(1/3)=fully reversed stress amplitude (or SIGMAar in the good man equation).
Mean stress is replaced with mean von-mises stress (same equation, different stresses)
Ultimate stress is replaced with (sqrt(2)/3)*SIGMA(u) or the von mises stress at failure.
Equations:
That last equation should be sqrt(2)/3. Made a mistake when writing the equations. Thanks.
Is this correct?