Femme_physics
Gold Member
- 2,548
- 1
Homework Statement
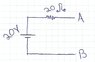
With respect to the attached drawing of an open circuit, which statement/s is/are true?
A) The circuit is open therefor no current flows in it
B) Vab = 0
C) Vab strives to infinity
D) Kirchhoff's current law does not apply on an open circuit
E) Vab = 20V
F) The voltage potential on the resistor equals 20V
G) The voltage potential on the circuit equals 0V
H) The flows in the circuit equals 1mA
The Attempt at a Solution
A) True
B) False, potential difference is about difference, not current.
C) I have a feeling that's false-- my theory is that the potential difference in terminals always equals to the potential difference in the battery.
D) No, Kirchhoff's law is always applied
E) True, based on my theory at C
F) True. I = 20/20. V = 20x1 V = 20 [V]
G) Not, that's 20. That's what we're told the difference is, it doesn't change.
H) False. It equals 1 Ampere (20 divided by 20), not miliampere.
Am I correct in everything?