Optics: light refraction in prisms

Click For Summary
SUMMARY

The discussion centers on the analysis of light refraction in prisms, specifically addressing discrepancies between a textbook approximation and a user's detailed method. The user initially questioned their approach, noting a significant difference in results. Feedback indicated that the textbook may have assumed a different orientation of the prism relative to the wall, which was not clearly stated in the problem. Ultimately, the user resolved their confusion regarding the approximation's applicability to their scenario.

PREREQUISITES
  • Understanding of light refraction principles
  • Familiarity with geometric optics
  • Knowledge of prism orientation effects
  • Ability to analyze optical diagrams
NEXT STEPS
  • Research the Snell's Law application in prism refraction
  • Explore the impact of prism orientation on light paths
  • Study common approximations used in optical textbooks
  • Investigate advanced optical simulation tools for accurate modeling
USEFUL FOR

Students of physics, optical engineers, and educators seeking to deepen their understanding of light behavior in prisms and the implications of approximations in optical calculations.

alingy1
Messages
325
Reaction score
0
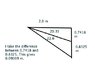
Could you please check the following problem?
The book made an approximation. I didn't in my method. But the difference seems considerable. Did I make a mistake?
 

Attachments

  • Screen Shot 2014-08-08 at 8.42.30 AM.png
    Screen Shot 2014-08-08 at 8.42.30 AM.png
    21.2 KB · Views: 558
  • Screen Shot 2014-08-08 at 8.42.43 AM.png
    Screen Shot 2014-08-08 at 8.42.43 AM.png
    7.6 KB · Views: 560
  • Lol.jpg
    Lol.jpg
    9.5 KB · Views: 520
Physics news on Phys.org
Your analysis looks good. I think maybe the textbook was assuming a different relative orientation between the prism and the wall. See attached figure. But the problem statement is not clear on this point.
 

Attachments

  • prism.png
    prism.png
    3.6 KB · Views: 532
EDIT: I get it now.
But, would using that approximation be fine for my picture?
 

Similar threads

Is this an oversimplification? (treating a lens as a set of prisms)
  • · Replies 10 ·
Replies
10
Views
1K
Lens Maker's Formula - Confusion in the derivation
  • · Replies 15 ·
Replies
15
Views
2K
Optical path difference between two reflected rays
  • · Replies 4 ·
Replies
4
Views
990
What is the refraction index of liver?
  • · Replies 5 ·
Replies
5
Views
2K
Calculate a radius of a circle on a screen
  • · Replies 3 ·
Replies
3
Views
1K
How do dark spot and tiny hole filters affect Fourier optics images?
  • · Replies 4 ·
Replies
4
Views
1K
How do I find the refractive index in sugar solutions?
  • · Replies 13 ·
Replies
13
Views
4K
How do I find refractive index uncertainties?
  • · Replies 3 ·
Replies
3
Views
4K
Graduate When should I analyze optical problems using ray tracing vs. wavefront analysis?
  • · Replies 12 ·
Replies
12
Views
2K
Light rays passing through a glass prism
  • · Replies 2 ·
Replies
2
Views
2K