Optics [refraction] - What is the actual angle from the surface of the water

[Paulo Serrano]

Homework Statement

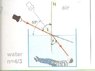
[PLAIN]http://img203.imageshack.us/img203/3072/refractiong.jpg

The apparent angle from the water is 53 degrees, but what is the actual angle from the water?

Homework Equations

n1 * sin i = n2 * sin r

The Attempt at a Solution

I think the real problem here is I'm not seeing some basic geometry stuff. The answer is 37 degrees.

 

[kuruman]

Which angle in the drawing is "the actual angle from the water"? How is it defined? Does it help to point out the numerological result that 53^o+37^o=90^o?

 

[Paulo Serrano]

That "actual angle" is the angle from the horizontal line (the water line) and the red line representing the light from the lamp (the one that is smaller than 53 degrees).

And yeah, I guess it makes sense than 90-53=37, but why that is the right answer I do not know.

 

[kuruman]

OK, can you find the 53^o angle somewhere between the lines you have drawn below the surface of the water? Look at your drawing. The continuation of the lines that form the 53^o in air, form what angle on the other side? How is that related to the angle of refraction?

 

[ehild]

To help Kuruman, I modified your picture, showing the angle of incidence (i) and the angle of refraction (r). Look at the drawing, and find the value of r.

ehild