ed1234
- 2
- 0
Homework Statement
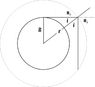
The refractive index of the Earth's atmosphere is:
n=1.01+(alpha)(R-r)
where (alpha) is a constant, r is radial distance from Earth's centre and R is the Earth's radius. By considering a path comprising a series of total internal reflections or otherwise, find a value of alpha for which a light ray emitted horizontally close to the Earth's surface would go around the Earth.
The Earth may be taken to be a perfect sphere radius R and the effects of absorption ignored).
Homework Equations
n1sin(theta1)=n2sin(theta2)
The Attempt at a Solution
I'm really fairly stuck on this on. I think we're looking for a gradient of refractive index such that the curvature of the light ray is equal to the curvature of the Earth but I'm not sure how to go about doing this quantitativly. Any hints/help would be appreciated.
Thanks